Cho a, b là 2 số thực khác 0. Biết 1 125 a 2 + 4 a b = 625 3 3 a 2 - 10 a b . Tính tỉ số a b .
A. 76 21
B. 2
C. 4 21
D. 76 3
Cho a, b là 2 số thực khác 0. Biết 1 125 a 2 + 4 a b = 625 3 3 a 2 - 10 a b . Tính tỉ số a b
A. 76 21
B. 2
C. 4 21
D. 76 3
Chọn C.
Phương pháp: Biến đổi đưa về cùng cơ số.
Cách giải: Vì a, b là 2 số thực khác 0 nên ta có:
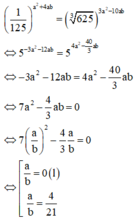
Cho biết a,b,c là các số thực khác 0. Biết x=1011ab2c3 và y=-2a2b2c là 2 số cùng dấu. Hỏi a là số dương hay âm?
Cho biết a,b,c là các số thực khác 0. Biết x=1011ab2c3 và y=-2a2b2c là 2 số cùng dấu. Hỏi a là số dương hay âm?
1.Tìm tất cả các số nguyên tố p sao cho só 2p+2 là tích 2 số tự nhên liên tiếp
2.Cho a, b, c, d là 4 số thực đôi 1 khác nhau. Biết rằng a,b là 2 nghiệm của phương trình \(x^2+mx+1=0\) (m, n là 2 số thực).
CM pt \(\left(a-c\right)\left(b-c\right)x^2+2\left(a-b\right)\left(c-d\right)x+\left(a-d\right)\left(d-b\right)=0\)
có 2 nghiệm thực phân biệt
Cho a,b là các số thực khác 0 thỏa mãn \(a\sqrt{2-b^2}+b\sqrt{2-a^2}=2\)
tìm min P = \(\dfrac{1}{a}+\dfrac{1}{b}-a-b\)
Cho a,b là các số thực khác 0 thỏa mãn \(a\sqrt{2-b^2}+b\sqrt{2-a^2}=2\)
Tìm Min :
P=\(\dfrac{1}{a}+\dfrac{1}{b}-a-b\)
Cho a,b là các số thực khác 0 thỏa mãn \(a\sqrt{2-b^2}+b\sqrt{2-a^2}=2\)
Tìm min của:
P=\(\dfrac{1}{a}+\dfrac{1}{b}\) - a - b
Cho a và b là các số thực khác 0 Biết \(\lim\limits_{x\rightarrow-\infty}\left(ax+b-\sqrt{x^2-6x+2}\right)=5\). Số lớn hơn trong hai số a và b là
A/ 4 B. 3 C.2 D. 1
Giới hạn đã cho hữu hạn nên \(a=-1\)
\(\lim\limits_{x\rightarrow-\infty}\dfrac{\left(b-x\right)^2-\left(x^2-6x+2\right)}{b-x+\sqrt{x^2-6x+2}}=\lim\limits_{x\rightarrow-\infty}\dfrac{\left(6-2b\right)x+b^2-2}{-x+\sqrt{x^2-6x+2}+b}\)
\(=\lim\limits_{x\rightarrow-\infty}\dfrac{6-2b+\dfrac{b^2-2}{x}}{-1-\sqrt{1-\dfrac{6}{x}+\dfrac{2}{x^2}}+\dfrac{b}{x}}=\dfrac{6-2b}{-2}=5\)
\(\Rightarrow b=8\)
Cả 4 đáp án đều sai, số lớn hơn là 8
Cho a,b,c là cac số thực khác 0 , tổng bằng 0
Tinh S = 1/b^2+c^2-a^2 + 1/c^2+ a^2 -b^2 + 1/a^2 +b^2 -c^2
Vì a+b+c=0
\(\Rightarrow a=-\left(b+c\right)\)
\(\Rightarrow a^2=\left[-\left(b+c\right)\right]^2=b^2+2bc+c^2\)
Do đó \(\frac{1}{b^2+c^2-a^2}=\frac{1}{b^2+c^2-b^2-2bc-c^2}=-\frac{1}{2bc}\)
Tương tự \(\frac{1}{c^2+a^2-b^2}=-\frac{1}{2ca}\) và \(\frac{1}{a^2+b^2-c^2}=-\frac{1}{2ab}\)
Do đó \(S=-\frac{1}{2}\left(\frac{1}{ab}+\frac{1}{bc}+\frac{1}{ca}\right)=-\frac{1}{2}.\frac{a+b+c}{abc}=0\)