Cho tứ diện ABCD có BC=a, CD=a 3 , B C D ^ = A B C ^ = A D C ^ = 90 ° . Góc giữa đường thẳng AD và BC bằng 60 ° . Tính bán kính R của mặt cầu ngoại tiếp tứ diện ABCD.
![]()
![]()
Tứ diện ABCD. Các điểm A'B'C'D' là điểm chia AB, BC, CD, DA theo tỉ số k (k≠1). Chứng minh tứ diện ABCD và tứ diện A'B'C'D' có cùng trọng tâm
Cho hình tứ diện ABCD có AB, BC, CD đôi một vuông góc. Điểm cách đều bốn điểm A, B, C, D là:
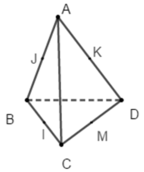
A. trung điểm J của AB
B. trung điểm I của BC
C. trung điểm K của AD
D. trung điểm M của CD
CD ⊥ (ABC) vì CD ⊥ AB và CD ⊥ BC
AB ⊥ (BCD) vì AB ⊥ BC và AB ⊥ CD
Phương án A sai vì tam giác ABC không vuông góc tại C nên trung điểm của AB không cách đều ba điểm A, B, C
Phương án B sai vì tam giác ABC không vuông góc tại A nên trung điểm của BC không cách đều ba điểm A, B, C
Phương án C đúng vì tam giác ACD vuông góc tại C nên trung điểm K của AD cách đều ba điểm A, C, D; tam giác ABD vuông góc tại B nên trung điểm K của AD cách đều ba điểm A, B và D
Phương án D sai vì tam giác CBD không vuông góc tại B nên trung điểm của CD không cách đều ba điểm B, C, D.
Đáp án C
Cho tứ diện ABCD có AD = BC = a, BD = CA = b, CD = AB = c. Tính V ABCD theo a, b, c
Đặt AC' = x, AD' = y, AA' = z.
Ta có:
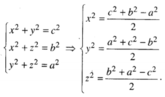
Từ đó suy ra V ABCD = V AC ' BD ' . A ' CB ' D / 3
Cho tứ diện ABCD có AB=CD=a . M, N lần lượt là trung điểm của BC, AD. Thể tích khối tứ diện ABCD là \(\dfrac{a^3\sqrt{3}}{12}\)và d(AB,CD)=a. Hãy tính MN
Cho tứ diện ABCD có AD = BC = a, BD = CA = b, CD = AB = c. Chứng minh rằng tâm các mặt cầu nội tiếp và ngoại tiếp của tứ diện ABCD trùng nhau. Tính bán kính của các mặt cầu đó theo a, b, c.
Ta có O là tâm của hình hộp chữ nhật AC'BD'.A'C'B'D nên nó là tâm của mặt cầu ngoại tiếp tứ diện ABCD. Bán kính của mặt cầu ngoại tiếp tứ diện ABCD là
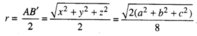
Gọi H và K theo thứ tự là chân đường vuông góc kẻ từ O đến (ABC) và (ABD). Vì OA = OB = OC nên HA = HB = HC, tương tự KA = KB = KD. Vì ΔABD = ΔBAC nên HA = KA. Do đó OH = OK. Tương tự, ta chứng minh được khoảng cách từ O đến các mặt của tứ diện ABCD bằng nhau nên O cũng là tâm của mặt cầu nội tiếp tứ diện ABCD.
Khi đó ta có V ABCD = V OABC + V OBCD + V OCDA + V ODAB
= 4 V OABC = 4 r ' S ABC / 3
Do đó:
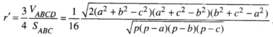
Trong đó 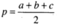
Cho tứ diện ABCD có AB=CD=a, AC=BD=b, AD=BC=c. Khoảng cách giữa hai đường thẳng AB và CD là
A. 1 2 b 2 + c 2 - a 2
B. 1 2 b 2 + c 2 + a 2
C. 1 4 b 2 + c 2 - a 2
D. 1 4 b 2 + c 2 + a 2
Chọn A
Gọi M,N lần lượt là trung điểm của AB và CD.
Khi đó
![]()
Cho tứ diện ABCD có A B = C D = a , A C = B D = b , A D = B C = c . Khoảng cách giữa hai đường thẳng AB và CD là
![]()
![]()
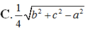
Cho tứ diện ABCD có AC=AD=BC=BD, AB=a, CD= a 3 Khoảng cách giữa hai đường thẳng AB và CD bằng a . Tính khoảng cách h từ điểm cách đều 4 đỉnh A,B,C,D đến mỗi đỉnh đó
A. h = a 13 2
B. h = a 13 4
C. h = a 3 2
D. h = a 3 4
Cho tứ diện ABCD có A B = A D = B C = B D , A B = a , C D = a 30 . Khoảng cách giữa hai đường thẳng AB và CD bằng a. Tính khoảng cách h từ điểm cách đều 4 đỉnh A, B, C, D đến mỗi đỉnh đó.
A. h = a 13 2
B. h = a 13 4
C. h = a 3 2
D. h = a 3 4
Chọn B
Gọi I là trung điểm AB, J là trung điểm CD
Từ AC=AD=BC=BD =>IJ chính là đoạn vuông góc chung của 2 đường thẳng AB và CD
=> IJ = a
Gọi O là điểm cách đều 4 đỉnh => O là tâm mặt cầu ngoại tiếp tứ diện ABCD
=> O nằm trên IJ => Ta cần tính OA
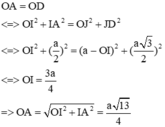
Ta có: