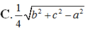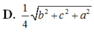Các câu hỏi tương tự
Hình hộp
A
B
C
D
.
A
,
B
,
C
,
D
,
có
A
B
A
A
,
A
D
a
và
A
,
A
B...
Đọc tiếp
Hình hộp A B C D . A , B , C , D , có A B = A A , = A D = a và A , A B ⏜ = A , A D ⏜ = B A D ⏜ = 60 0 Khoảng cách giữa các đường thẳng chứa các cạnh đối diện của tứ diện A , A B D bằng

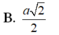
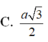
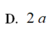
Cho
d
1
,
d
2
chéo nhau và khoảng cách
d
1
,
d
2
3
. Biết
d
1
∥
v
1
→...
Đọc tiếp
Cho d 1 , d 2 chéo nhau và khoảng cách d 1 , d 2 = 3 . Biết d 1 ∥ v 1 → = 2 ; - 1 ; 1 ; d 1 ∥ v 2 → = 1 ; 1 ; 2 ; A , B ∈ d 1 và C , D ∈ d 2 sao cho A B = C D = 2 . Biết tứ diện ABCD có thể tích V không phụ thuộc việc chọn các điểm A, B, C, D. Tính V.
![]()
![]()
![]()
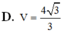
Cho tứ diện đều ABCD có tất cả các cạnh bằng a. Khoảng cách giữa hai đường thẳng AB và CD là: A.
a
2
2
B.
a
3
2
C.
a
3
2
D. a
Đọc tiếp
Cho tứ diện đều ABCD có tất cả các cạnh bằng a. Khoảng cách giữa hai đường thẳng AB và CD là:
A. a 2 2
B. a 3 2
C. a 3 2
D. a
Cho tứ diện đều ABCD có cạnh a. Tính khoảng cách giữa hai đường thẳng AB và CD.
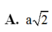
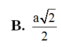
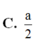
![]()
Trong không gian với hệ tọa độ , cho hai đường thẳng Trên đường thẳng d1 lấy hai điểm A, B thỏa mãn AB 3 . Trên đường thẳng d2 lấy hai điểm C, D thỏa mãn CD 4. Tính thể tích C của tứ diện ABCD. A. V 7 B. V 2√21 C.
V
4
21
3
D.
V
5...
Đọc tiếp
Trong không gian với hệ tọa độ , cho hai đường thẳng
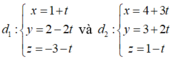
Trên đường thẳng d1 lấy hai điểm A, B thỏa mãn AB = 3 . Trên đường thẳng d2 lấy hai điểm C, D thỏa mãn CD = 4. Tính thể tích C của tứ diện ABCD.
A. V = 7
B. V = 2√21
C. V = 4 21 3
D. V = 5 21 6
Cho tứ diện đều ABCD cạnh bằng a. Khoảng cách d giữa hai đường thẳng AD và BC là A.
d
a
3
2
B.
d
a
2
2
C.
d
a
2
3
D.
d
a...
Đọc tiếp
Cho tứ diện đều ABCD cạnh bằng a. Khoảng cách d giữa hai đường thẳng AD và BC là
A. d = a 3 2
B. d = a 2 2
C. d = a 2 3
D. d = a 3 3
Cho tứ diện đều ABCD cạnh a, tính khoảng cách giữa hai đường thẳng AB và CD. A.
a
2
2
B.
a
3
2
C.
a
3...
Đọc tiếp
Cho tứ diện đều ABCD cạnh a, tính khoảng cách giữa hai đường thẳng AB và CD.
A. a 2 2
B. a 3 2
C. a 3 3
D. a
Cho tứ diện đều ABCD cạnh a, tính khoảng cách giữa hai đường thẳng AB và CD. A.
a
2
2
B.
a
3
2
C.
a
3...
Đọc tiếp
Cho tứ diện đều ABCD cạnh a, tính khoảng cách giữa hai đường thẳng AB và CD.
A. a 2 2
B. a 3 2
C. a 3 3
D. a
Cho hai đường thẳng chéo nhau d và d’. Đoạn thẳng AB có độ dài bằng a trượt trên d, đoạn thẳng CD có độ dài bằng b trượt trên d’. Chứng minh rằng khối tứ diện ABCD có thể tích không đổi.