Số nghiệm của phương trình \(\sin \left( {x + \frac{\pi }{4}} \right) = \frac{{\sqrt 2 }}{2}\) trên đoạn \(\left[ {0;\pi } \right]\) là:
A.4
B.1
C.2
D.3
Ta có
\(\begin{array}{l}\sin \left( {x + \frac{\pi }{4}} \right) = \frac{{\sqrt 2 }}{2}\\ \Leftrightarrow \sin \left( {x + \frac{\pi }{4}} \right) = \sin \left( {\frac{\pi }{4}} \right)\\ \Leftrightarrow \left[ \begin{array}{l}x + \frac{\pi }{4}{\rm{ }} = {\rm{ }}\frac{\pi }{4} + k2\pi ;k \in Z\\x + \frac{\pi }{4}{\rm{ }} = {\rm{ }}\pi {\rm{ - }}\frac{\pi }{4} + k2\pi ;k \in Z\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = {\rm{ }}k2\pi ;k \in Z\\x{\rm{ }} = {\rm{ }}\frac{\pi }{2} + k2\pi ;k \in Z\end{array} \right.\end{array}\)
Mà \(x \in \left[ {0;\pi } \right]\) nên \(x \in \left\{ {0;\frac{\pi }{2}} \right\}\)
Vậy phương trình đã cho có số nghiệm là 2.
Chọn C
Số nghiệm thuộc đoạn 0 , 5 π 2 của phương trình 2.sin x – 1 = 0 là
A. 2
B. 3
C. 1
D. 4
Số nghiệm chung của hai phương trình 4 cos 2 x − 3 = 0 và 2.sin x + 1 = 0 trên khoảng − π 2 ; 3 π 2 là:
A. 4
B. 1
C. 2
D. 3
Số nghiệm chung của hai phương trình 4 cos 2 x - 3 = 0 và 2 sin x + 1 = 0 trên khoảng - π 2 ; 3 π 2 là:
A. 4.
B. 1.
C. 2
D. 3.
Đáp án C
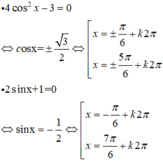
Vậy 2 pt trên có 2 họ nghiệm chung là:
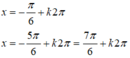
Tính tổng tất cả các nghiệm của phương trình sin x + sin 2 x = 0 trên đoạn [0;2p ].
A. 4p .
B. 5p .
C. 3p .
D. 2p .
Tính tổng các nghiệm của phương trình
sin 2x + 4sin x - 2cos x - 4 = 0 trên đoạn 0 ; 100 π
A. 2476 π
B. 25 π
C. 2475 π
D. 100 π
Đáp án C
2sin x cos x + 4 sin x - 2 cos x - 4 = 0
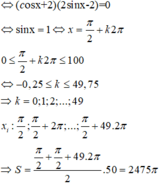
Câu 33 : số nghiệm của phương trình 3cos x + 2=0 trên đoạn [0;5π] là: A. 4 B. 3 C. 6 D. 5 Câu 34. Số nghiệm của phương trình ( 2cos^2 x - cos x)/ (tan x -√3)=0 trên đoạn [0;3] là A. 4 B. 3 C. 2 D. 1
Gọi S là tổng các nghiệm của phương trình sin x cos x + 1 = 0 trên đoạn 0 ; 2017 π .Tính S.
A. S = 2035153 π
B. S = 1001000 π
C. S = 1017072 π
D. S = 200200 π
Tìm số nghiệm thuộc đoạn 2 π , 4 π của phương trình sin 2 x cos x + 1 = 0
A. 5
B. 6
C. 3
D. 4
Dùng đồ thị hàm số y = sinx, y = cosx để xác định số nghiệm của phương trình:
a) \(3\sin x + 2 = 0\) trên đoạn \(\left( { - \frac{{5\pi }}{2};\frac{{5\pi }}{2}} \right)\)
b) \(\cos x = 0\) trên đoạn \(\left[ { - \frac{{5\pi }}{2};\frac{{5\pi }}{2}} \right]\)
a) Vẽ đồ thị:
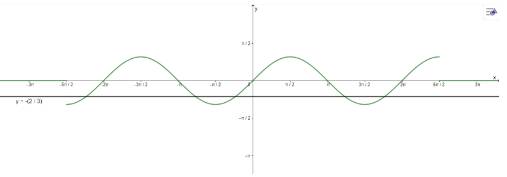
\(3\sin x + 2 = 0\) trên đoạn \(\left( { - \frac{{5\pi }}{2};\frac{{5\pi }}{2}} \right)\) có 5 nghiệm
b) Vẽ đồ thị:
\(\cos x = 0\) trên đoạn \(\left[ { - \frac{{5\pi }}{2};\frac{{5\pi }}{2}} \right]\) có 6 nghiệm
