Gọi BM, CN là 2 đường trung tuyến của \(\Delta ABC\)

\( \Rightarrow \)MA = MC = \(\dfrac{1}{2}\)AC; NA = NB = \(\dfrac{1}{2}\)AB

Vì \(\Delta ABC\) cân tại A nên AB = AC ( tính chất)

Do đó, AM = MC = NA = NB

Xét \(\Delta \)ANC và \(\Delta \)AMB, ta có:

AN = AM

\(\widehat A\) chung

AC = AB

\( \Rightarrow \)\(\Delta \)ANC = \(\Delta \)AMB (c.g.c)

\( \Rightarrow \) NC = MB ( 2 cạnh tương ứng)

Vậy 2 đường trung tuyến ứng với 2 cạnh bên của tam giác cân là hai đoạn thẳng bằng nhau.

Vì \(∆ABC\) có hai đường trung tuyến \(BM\) và \(CN\) cắt nhau ở \(G\)

\(\Rightarrow \) \(G\) là trọng tâm của tam giác \(ABC\).

\(\Rightarrow  GB = \dfrac{2}{3}BM\); \(GC = \dfrac{2}{3}CN\) ( tính chất đường trung tuyến trong tam giác)

Mà \(BM = CN\) (giả thiết) nên \(GB = GC.\)

Tam giác \(GBC\) có \(GB = GC\) nên \(∆GBC\) cân tại \(G\).

\(\Rightarrow \) \(\widehat{GCB} = \widehat{GBC}\) (Tính chất tam giác cân).

Xét \(∆BCN\) và \(∆CBM\) có: 

+) \(BC\) là cạnh chung

+) \(CN = BM\) (giả thiết)

+) \(\widehat{GCB} = \widehat{GBC}\) (chứng minh trên)

Suy ra \(∆BCN = ∆CBM\) (c.g.c)

 \(\Rightarrow \) \(\widehat{NBC} = \widehat{MCB}\) (hai góc tương ứng).

\(\Rightarrow ∆ABC\) cân tại \(A\) (tam giác có hai góc bằng nhau là tam giác cân)

#\(N\)

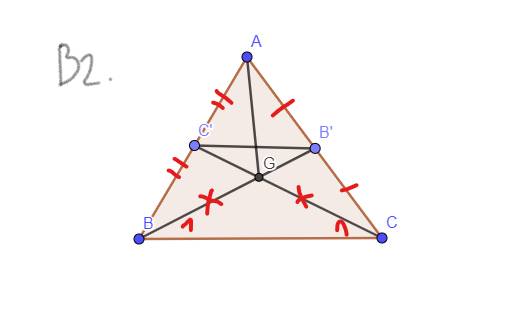
`a,` `GT: AB = AC,` \(\widehat{B}=\widehat{C}\)

`CM: BB' = C``C'`

`BB'` là đường trung tuyến

`-> B'` là trung điểm của `AC`

`-> AB' = B'C` 

`C``C'` là đường trung tuyến

`-> C'` là trung điểm của `AB`

`-> AC' = C'B`

Tam giác `ABC` cân tại `A`

`-> AB = AC`

`-> AC' = AB' = C'B = B'C`

Xét Tam giác `BB'C` và Tam giác `C``C'B:`

`C'B = B'C`

\(\widehat{B}=\widehat{C}\)

`BC` chung

`=>` Tam giác `BB'C =` Tam giác `C``C'B (c-g-c)`

`=> BB' = C``C' (2` cạnh tương ứng `) (đpcm)`

`b, GT: AB' = B'C ; AC'=C'B ; C``C' = BB'`

`KL:` Tam giác `ABC` cân

`BB', C``C'` là đường trung tuyến

giả sử: `BB'` cắt `C``C'` tại `G`

`-> G` là trọng tâm của Tam giác `ABC`

`-> GB = 2/3 BB'`

`-> GC = 2/3 C``C'`

`BB' = C``C' -> GB = GC`

`->` Tam giác `GBC` cân tại `G`

`->`\(\widehat{B_1}=\widehat{C_1}\) 

Xét Tam giác `BB'C` và Tam giác `C``C'B` có:

`BB' = C``C'`

\(\widehat{B_1}=\widehat{C_1}\)

`BC` chung

`=>`Tam giác `BB'C =` Tam giác `C``C'B (c-g-c)`

`-> BC' = B'C`

`-> 1/2 AB = 1/2 AC`

`-> AB = AC`

`->` Tam giác `ABC` cân tại `A (đpcm)`.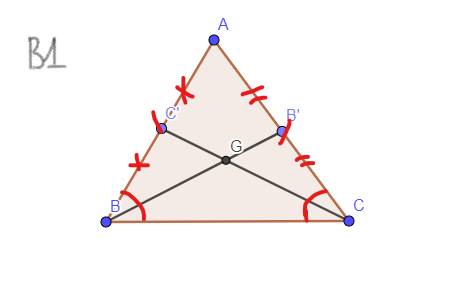

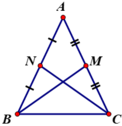
giúp mình với

a: ΔABC cân tại A có BM,CN là các trung tuyến

Xét ΔABM và ΔACN có

AB=AC
góc A chung

AM=AN

=>ΔABM=ΔACN

=>BM=CN

b: Gọi G là giao của BM và CN

=>G là trọng tâm của ΔABC

=>GB=2/3BM; GC=2/3CN

mà BM=CN

nên GB=GC

=>góc GBC=góc GCB

Xét ΔNBC và ΔMCB có

NC=MB

BC chung

góc NCB=góc MBC

=>ΔNBC=ΔMCB

=>góc ABC=góc ACB

=>ΔBAC cân tại A

Giả sử ΔABC cân tại A có hai đường trung tuyến BM và CN, ta cần chứng minh BM = CN.

Ta có: AC = 2.AM, AB = 2. AN, AB = AC (vì ΔABC cân tại A)

⇒ AM = AN.

Xét ΔABM và ΔACN có:

AM = AN

AB = AC

Góc A chung

⇒ ΔABM = ΔACN (c.g.c) ⇒ BM = CN (hai cạnh tương ứng).

(Còn một số cách chứng minh khác, nhưng do giới hạn kiến thức lớp 7 nên mình xin sẽ không trình bày.)

Giả sử ∆ABC  cân tại A có hai đường trung tuyến BM và CN, ta chứng minh BM = CN

Vì ∆ ABC cân tại A=>  AB = AC mà M, N là trung điểm AC, AB nên CM = BN

Do đó ∆CMB ;∆BNC có:

BC chung

CM = BN (cm trên)

AB = AC (∆ABC  cân)

=> BM = CN (đpcm)

Giả sử ∆ABC  cân tại A có hai đường trung tuyến BM và CN, ta chứng minh BM = CN

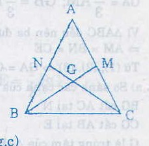
Vì ∆ ABC cân tại A=>  AB = AC mà M, N là trung điểm AC, AB nên CM = BN

Do đó ∆CMB ;∆BNC có:

BC chung

CM = BN (cm trên)

AB = AC (∆ABC  cân)

=> BM = CN

Giả sử ∆ABC  cân tại A có hai đường trung tuyến BM và CN, ta chứng minh BM = CN

Ta có AN = NB = AB/2 (Tính chất đường trung tuyến)

AM = MC = AC/2 (Tính chất đường trung tuyến)

Vì ∆ ABC cân tại A=>  AB = AC nên AM = AN

Xét  ∆BAM ;∆CAN có:

AM = AN  (cm trên)

Góc A chung

AB = AC (∆ABC  cân)

Nên suy ra ∆BAM = ∆CAN (c-g-c)

=> BM = CN ( 2 cạnh tương ứng)

Giả sử ∆ABC cân tại A có hai đường trung tuyến BM và CN, ta chứng minh BM = CN

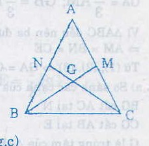
Vì ∆ ABC cân tại A=> AB = AC mà M, N là trung điểm AC, AB nên CM = BN

Do đó ∆CMB ;∆BNC có:

BC chung

CM = BN (cm trên)

AB = AC (∆ABC cân)

=> BM = CN

tick mk di bao gio mk hoc roi thi mk giai cho

nếu trong định lí ghi vậy thì chắc chắn điều này luồn đúng, đéo cần chứng minh cũng biết

Su dung cac tinhchat tam giac can ma cm 2 tam giac bang nhau

Duong trung tuyen la dg trung trc,,Duong cao ,,,,ra dc ma

Tick mik nke