Xét sự đồng biến, nghịch biến của các hàm số: y = 16x + 2 x 2 − 16 x 3 /3 − x 4

Những câu hỏi liên quan
Xét sự đồng biến, nghịch biến của các hàm số:a) y 3
x
2
− 8
x
3
b) y 16x + 2
x
2
− 16
x
3
/3 −
x
4
c) y
x
3
− 6
x
2
+ 9xd) y
x
4
+ 8...
Đọc tiếp
Xét sự đồng biến, nghịch biến của các hàm số:
a) y = 3 x 2 − 8 x 3
b) y = 16x + 2 x 2 − 16 x 3 /3 − x 4
c) y = x 3 − 6 x 2 + 9x
d) y = x 4 + 8 x 2 + 5
a) TXĐ: R
y′ = 6x − 24 x 2 = 6x(1 − 4x)
y' = 0 ⇔ 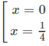
y' > 0 trên khoảng (0; 1/4) , suy ra y đồng biến trên khoảng (0; 1/4)
y' < 0 trên các khoảng ( - ∞ ; 0 ); (14; + ∞ ), suy ra y nghịch biến trên các khoảng ( - ∞ ;0 ); (14; + ∞ )
b) TXĐ: R
y′ = 16 + 4x − 16 x 2 − 4 x 3 = −4(x + 4)( x 2 − 1)
y' = 0 ⇔ 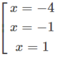
Bảng biến thiên:
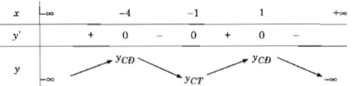
Vậy hàm số y đã cho đồng biến trên các khoảng ( - ∞ ; -4) và (-1; 1), nghịch biến trên các khoảng (-4; -1) và (1; + ∞ )
c) TXĐ: R
y′ = 3 x 2 − 12x + 9
y' = 0
y' > 0 trên các khoảng ( - ∞ ; 1), (3; + ∞ ) nên y đồng biến trên các khoảng ( - ∞ ; 1), (3; + ∞ )
y'< 0 trên khoảng (1; 3) nên y nghịch biến trên khoảng (1; 3)
d) TXĐ: R
y′ = 4 x 3 + 16 = 4x( x 2 + 4)
y' = 0 ⇔ 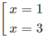
y' > 0 trên khoảng (0; + ∞ ) ⇒ y đồng biến trên khoảng (0; + ∞ )
y' < 0 trên khoảng ( - ∞ ; 0) ⇒ y nghịch biến trên khoảng ( - ∞ ; 0)
Đúng 0
Bình luận (0)
Xét sự đồng biến, nghịch biến của các hàm số: y = x − sinx, x ∈ [0; 2 π ].
y = x – sinx, x ∈ [0; 2 π ].
y′ = 1 – cosx ≥ 0 với mọi x ∈ [0; 2 π ]
Dấu “=” xảy ra chỉ tại x = 0 và x = 2 π .
Vậy hàm số đồng biến trên đoạn [0; 2 π ].
Đúng 0
Bình luận (0)
Xét sự đồng biến, nghịch biến của các hàm số :
a) \(y=3x^2-8x^3\)
b) \(y=16x+2x^2-\dfrac{16}{3}x^3-x^4\)
c) \(y=x^3-6x^2+9x\)
d) \(y=x^4+8x^2+5\)
Cho hàm số y=\(\left(3-2\sqrt{2}\right)x+\sqrt{2}-1\)
a) Xét sự đồng biến và nghịch biến của các hàm số trên;
b) Tính giá trị của y khi x=\(3+2\sqrt{2}\)
a) Vì \(3-2\sqrt{2}>0\) nên hàm số đồng biến
b) Thay \(x=3+2\sqrt{2}\) vào hàm số, ta được:
\(y=\left(3-2\sqrt{2}\right)\left(3+2\sqrt{2}\right)+\sqrt{2}-1\)
\(=9-8+\sqrt{2}-1\)
\(=\sqrt{2}\)
Đúng 2
Bình luận (0)
a) `a=3-2\sqrt2>0 =>` Hàm số đồng biến.
b) `y=(3-2\sqrt2)(3+2\sqrt2)+\sqrt2-1=3^2-(2\sqrt2)^2+\sqrt2-1=\sqrt2`
`=> y=\sqrt2` khi `x=3+2\sqrt2`
Đúng 1
Bình luận (0)
Xét sự đồng biến, nghịch biến của các hàm số: y = sin(1/x), (x > 0)
Xét hàm số y = sin(1/x) với x > 0.
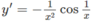
Giải bất phương trình sau trên khoảng (0; + ∞ ):
![]()
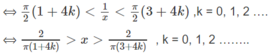
Do đó, hàm số đồng biến trên các khoảng
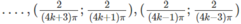
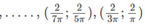
Và nghịch biến trên các khoảng
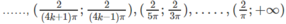
với k = 0, 1, 2 …
Đúng 0
Bình luận (0)
Xét sự đồng biến, nghịch biến của hàm số
a, y = \(x\sqrt{1-x^2}\)
b,y = \(\sqrt{3x^2-x^3}\)
Xét sự đồng biến, nghịch biến của các hàm số:
a) y = x − sinx, x ∈ [0; 2π].
c) y = sin(1/x), (x > 0)
a) y = x – sinx, x ∈ [0; 2π].
y′ = 1 – cosx ≥ 0 với mọi x ∈ [0; 2π]
Dấu “=” xảy ra chỉ tại x = 0 và x = 2π.
Vậy hàm số đồng biến trên đoạn [0; 2π].
c) Xét hàm số y = sin(1/x) với x > 0.
![]()
Giải bất phương trình sau trên khoảng (0; + ∞ ):
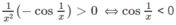
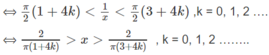
Do đó, hàm số đồng biến trên các khoảng
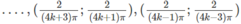
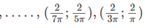
Và nghịch biến trên các khoảng
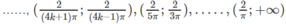
với k = 0, 1, 2 …
Đúng 0
Bình luận (0)
Xét sự đồng biến và nghịch biến của các hàm số :a. yleft(3sqrt{2}-sqrt{19}right)x+5b. y3left(x-1right)-sqrt{5}xc. yleft(2-sqrt{3}right)x-sqrt{2}x+1d. yleft(m^2-m+1right)x-2m( với m là tham số, x là biến ) Đối với những câu chưa chuyển sang dạng hàm số bậc nhất, chuyển sang hàm số bậc nhất rồi xét sự đồng biến, nghịch biến.
Đọc tiếp
Xét sự đồng biến và nghịch biến của các hàm số :
a. \(y=\left(3\sqrt{2}-\sqrt{19}\right)x+5\)
b. \(y=3\left(x-1\right)-\sqrt{5}x\)
c. \(y=\left(2-\sqrt{3}\right)x-\sqrt{2}x+1\)
d. \(y=\left(m^2-m+1\right)x-2m\)( với m là tham số, x là biến )
=> Đối với những câu chưa chuyển sang dạng hàm số bậc nhất, chuyển sang hàm số bậc nhất rồi xét sự đồng biến, nghịch biến.
xét sự đồng biến, nghịch biến của hàm số: y=sin 1/x (x>0)
kiểu bài này có đáp án trên mạng rồi ấy ạ, anh/chị/ bạn nào mà xem qua đáp án trên mạng có thể giải thích kĩ hơn giúp em chỗ cos 1/x >0 về đoạn sau được không ạ, chứ ai đọc mãi mà không hiểu được 😭😭
Đúng 0
Bình luận (0)
Bất phương trình lượng giác:
\(cos\left(X\right)\ge a\Leftrightarrow-arccos\left(a\right)+k2\pi\le X\le arccos\left(a\right)+k2\pi\)
Vậy BPT: \(cos\left(\dfrac{1}{x}\right)>0\)
\(\Leftrightarrow-\dfrac{\pi}{2}+k2\pi\le\dfrac{1}{x}\le\dfrac{\pi}{2}+k2\pi\) với \(k\ge1\)
Nghịch đảo: \(\dfrac{2}{k4\pi-\pi}\le x\le\dfrac{2}{k4\pi+\pi}\)
Đúng 0
Bình luận (0)

















