Ta có : Góc COA = góc AOE ; góc BOD = góc BOF

Mà góc BOD + góc COD + góc COA = 180 độ ; góc AOE + góc EOF + góc BOF = 180 độ

=> góc COD = góc EOF = 90 độ

=> OE vuông góc với OF

Chỉ cần chứng minh góc đấy ( FOE = 90 độ )

Do OC vuông góc với OD

\(\Rightarrow\widehat{COD}=90^o\)

    Do OA là tia p.g của \(\widehat{COE}\)

         OB là tia p.g của \(\widehat{DOF}\)

\(\Rightarrow\widehat{COD}\)đối đỉnh \(\widehat{EOF}\)

mà \(\widehat{COD}=90^o\)

\(\Rightarrow\widehat{EOF}=90^o\)

mà góc EOF = \(90^o\)

\(\Rightarrow\)OE vuông góc OF

Ta có:
- Góc AOE = BOE = 55 độ (do AOE = BO = 55 độ)
- Góc EOF = 180 - (AOE + BO) = 180 - (55 + 55) = 70 độ

Vì OM vuông góc với AB, nên góc MOE = góc MOF (do cùng là góc vuông).

Vậy, ta đã chứng minh được rằng tia OM là tia phân giác của góc EOF.

--thodagbun--

Các anh chị giúp em với ạ

góc AOC+góc BOC=180 độ

=>góc BOC=180-150=30 độ

góc AOD+góc BOD=180 độ

=>góc AOD=180-150=30 độ

góc AOD=góc BOE(hai góc đối đỉnh)

góc AOD=góc BOC(=30 độ)

=>góc BOC=góc BOE

=>OB là phân giác của góc COE

Để chứng minh OB là tia phân giác của COE, ta cần chứng minh OB cắt góc COE thành hai góc bằng nhau. Gọi M là trung điểm của OD. Ta có: - Góc AOC = 150 độ (theo đề bài) - Góc BOD = 150 độ (theo đề bài) - Góc COE = 180 độ - góc AOC = 180 độ - 150 độ = 30 độ (do AOC là góc bẹt) - Góc DOE = 180 độ - góc BOD = 180 độ - 150 độ = 30 độ (do BOD là góc bẹt) Vì góc COE = góc DOE = 30 độ, nên ta có: - Góc COM = góc DOM = 30 độ (do M là trung điểm của OD) - Góc COB = góc DOB = 150 độ (do OC và OD là hai tia đối của nhau) Vậy ta có: - Góc COM = góc COB = 30 độ - Góc DOM = góc DOB = 30 độ Do đó, OB là tia phân giác của COE.

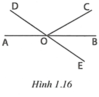
Hai góc AOC và BOC kề bù nên  A O C ^ + B O C ^ = 180 °

⇒ B O C ^ = 180 ° − 150 ° = 30 ° .

Tương tự, ta tính được A O D ^ = 30 ° .

Ta có B O E ^ = A O D ^ = 30 °  (hai góc đối đỉnh).

Suy ra B O C ^ = B O E ^ = 30 ° . (1)

Tia OB nằm giữa hai tia OC và OE. (2)

Từ (1) và (2) ta được tia OB là tia phân giác của góc COE

Đếm góc, đếm tia

Ta thấy: khi vẽ các tia OC, OD, OE, OF thì số góc là 5 góc.

Trung bình số đo mỗi góc là :

\(180^o:5=36^o\)

- Nếu có 1 góc có số đo lớn hơn \(36^o\)thì sẽ có ít nhất 1 góc có số đo \(\le36^o\)( đpcm )

Các TH còn lại là \(\le36^o\)thì thoản mãn. ( đpcm )