Cho tam giác ABC có BC = 11 cm, A B C ^ = 38 0 và A C B ^ = 30 0 . Gọi N là chân đường vuông góc hạ từ A xuông cạnh BC. Hãy tính:
a, Độ dài đoạn thẳng AN
b, Độ dài đoạn thang AC
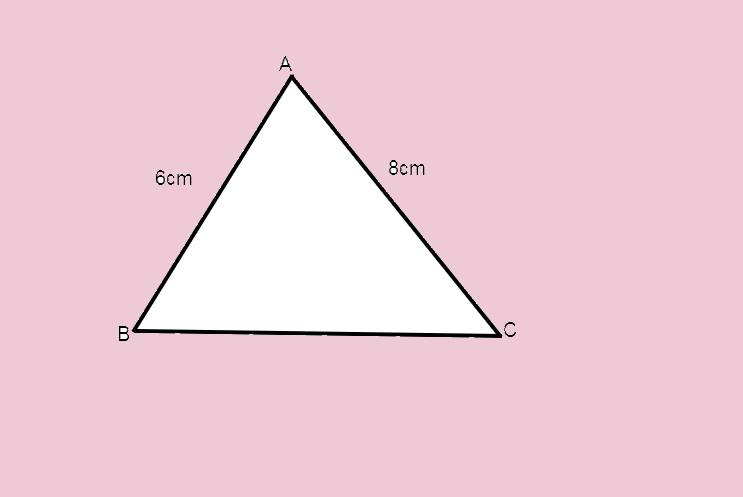
Cho tam giác ABC vuông ở A , có AB = 6 cm , AC = 8 cm . Độ dài cạnh BC là:
A. 9 cm B. 10 cm C. 11 cm D.12cm
Áp dụng định lý pytago cho tam giác `ABC` ta có :
`BC^2= AB^2+AC^2`
`BC^2=6^2+8^2`
`BC^2= 36+64`
`BC^2=100`
`=>BC=10(cm)`
`->B`
Cho tam giác ABC vuông tại A, có BC = a, AC = b, AB = c. Giải tam giác ABC, biết:
a, a = 15 cm, b = 10 cm
b, b = 12 cm, c = 7 cm
Cho tam giác ABC có N là trung điểm của AB ; M là trung điểm của AC ; BC = 22 cm thì NM = ? a. 11 cm b. 6 cm c. 24 cm d. Kết quả khác
Cho tam giác ABC có AB = 6 cm ; AC = 4,5 cm ; BC = 7,5 cm a) chứng minh tam giác ABC vuông tại A b) Kẻ đường cao AH (H thuộc BC) tính BH, HC, AH và góc B,C của tam giác c) Tính diện tích tam giác ABC d) tìm vị trí điểm M để diện tích tam giác ABC bằng diện tích tam giác MBC
a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
c: \(S_{ABC}=\dfrac{AB\cdot AC}{2}=\dfrac{6\cdot4.5}{2}=3\cdot4.5=13.5\left(cm^2\right)\)
Bài 2 : Cho tam giác ABC có AB=3cm; AC= 4cm; BC= 5cm . So sánh các góc của tam giác ABC
Bài 3 :Cho tam giác ABC có góc B=60 độ ; góc C = 40 độ . So sánh các cạnh của tam giác ABC
Bài 4 : Cho tam giác ABC có AB=5cm ; AC= 12 cm ; BC=13 cm
a) Tam giác ABC là tam giác gì ?
b) So sánh các góc của tam giác ABC
Bài 5 : Cho tam giác ABC vuông tại A có AB=10cm ; AC= 24 cm
a) Tính độ dài cạnh BC=?
b) Tam giác ABC là tam giác gì ?
bài 2:
ta có: AB<AC<BC(Vì 3cm<4cm<5cm)
=> góc C>góc A> góc B (Các cạnh và góc đồi diện trong tam giác)
Bài 3:
*Xét tam giác ABC, có:
góc A+góc B+góc c= 180 độ( tổng 3 góc 1 tam giác)
hay góc A+60 độ +40 độ=180độ
=> góc A= 180 độ-60 độ-40 độ.
=> góc A=80 độ
Ta có: góc A>góc B>góc C(vì 80 độ>60 độ>40 độ)
=> BC>AC>AB( Các cạnh và góc đối diện trong tam giác)
bài 2:
ta có: AB <AC <BC (Vì 3cm <4cm <5cm)
=> góc C>góc A> góc B (Các cạnh và góc đồi diện trong tam giác)
Bài 3:
*Xét tam giác ABC, có:
góc A+góc B+góc c= 180 độ( tổng 3 góc 1 tam giác)
hay góc A+60 độ +40 độ=180độ
=> góc A= 180 độ-60 độ-40 độ.
=> góc A=80 độ
Ta có: góc A>góc B>góc C(vì 80 độ>60 độ>40 độ)
=> BC>AC>AB( Các cạnh và góc đối diện trong tam giác)
HT mik làm giống bạn Dương Mạnh Quyết
ta có: AB<AC<BC(Vì 3cm<4cm<5cm)
=> góc C>góc A> góc B (Các cạnh và góc đồi diện trong tam giác)
Bài 3:
*Xét tam giác ABC, có:
góc A+góc B+góc c= 180 độ( tổng 3 góc 1 tam giác)
hay góc A+60 độ +40 độ=180độ
=> góc A= 180 độ-60 độ-40 độ.
=> góc A=80 độ
Ta có: góc A>góc B>góc C(vì 80 độ>60 độ>40 độ)
=> BC>AC>AB( Các cạnh và góc đối diện trong tam giác)
cho tam giác ABC vuông tại A . Có AB bằng 6 cm. AC bằng 8 cm. a tính độ dài cạnh BC và chu vi tam giác ABC . Đường phân giác của góc B cắt AC tại D .Vẽ DH vuông góc BC . [ H thuộc BC ]. CM tam giác ABD = tam giác HBD c CM DA < DC . có vẽ hình nha mọi người
a: BC=10cm
C=AB+BC+AC=6+8+10=24(cm)
b: Xét ΔABD vuông tại A và ΔHBD vuông tại H có
BD chung
\(\widehat{ABD}=\widehat{HBD}\)
Do đó: ΔABD=ΔHBD
c: Ta có: ΔABD=ΔHBD
nên DA=DH
mà DH<DC
nên DA<DC
Cho tam giác ABC cân tại A. Có AD là phân giác góc A (D thuộc BC)
a/ Cm tam giác ABD = tam giác ACD
b/ Cm Ad vuông góc BC
c/ Cho AB = 10 cm, BC = 16 cm. Tính AD
a,Xét tam giác abd và tam tam giác acd có
ab=ac
góc bad= góc cad
adchung
=>tam giác abd = tam giác acd (c.g.c)
b,vì tam giác abd=tam giác acd
=>góc adb =góc adc
mà góc adb + góc adc=180 độ
=>ad vuông góc với bc
c,bd=16:2=8cm
áp dụng định lí PY-TA-GO vào tam giác abd
ta có
ab^2=ad^2+bd^2
=>ad^2=ab^2-bd^2
=>ad=6cm
a) Xet tam giac ADB va tam giac ADC ta co
BA=CA theo gia thiet
goc BAD=goc ACD theo gia thiet
canh chung AD
nen suy ra:tam giac ADB=tam giac ADC theo truong hop canh goc canh
b) tu cau a ta co goc ADB= goc ADC hai goc tung ung
nen suy ra GOC ADB= gocADC =180:2=90DO
Vay ta co AD vuong goc voi BC
c)vi BD=1/2BC nen ta co BD =16:2 =8
vay theo dinh ly pi ta go ta co 10^2+8^2=100+64=164
nen ta co ADbang can bac 2 cua 164
Cho tam giác ABC có AB=6 cm ; AC = 4,5 cm : BC= 7,5 cm
a) Chứng minh tam giác ABC vuông ở A
Tính góc B ; góc C ; đường cao AH của tam giác ABC
b) Tìm tập hợp điểm M sao cho S tam giác ABC = S tam giác BMC
Cho tam giác \(ABC\) có \(BC=15\) \(cm\), \(AC=20\) \(cm\), \(AB=25\) \(cm\).
\(a\). Tính độ dài đường cao \(CH\) của tam giác \(ABC\).
\(b\). Gọi \(CD\) là đường phân giác của tam giác \(ACH\). Chứng minh tam giác \(BCD\) cân.
\(c\). Chứng minh: \(BC^2+CD^2+BD^2=3CH^2+2BH^2+DH^2\)
a: Xét ΔCAB có CA^2+CB^2=AB^2
nên ΔCAB vuông tại C
Xét ΔCAB vuông tại C có CH là đường cao
nên CH*AB=CA*CB
=>CH*25=15*20=300
=>CH=12(cm)
b: góc BCD+góc ACD=90 độ
góc BDC+góc HCD=90 độ
mà góc ACD=góc HCD
nên góc BCD=góc BDC
=>ΔBDC cân tại B
c: BC^2+BD^2+CD^2
=BC^2+BC^2+CD^2
=2BC^2+CD^2
=2(BH^2+HC^2)+CH^2+HD^2
=2BH^2+3CH^2+DH^2
Cho tam giác ABC có AB = 12cm, AC = 9cm, BC = 15cm. Kẻ đường cao AH.
a)Cm tam giác ABC là tam giác vuông. AH = ?
b)Kẻ HK vuông góc AC. Cm Tam giác KAH ~ Tam giác ABC
c)Cm : IK . AC = KH . BC