ta có g A1 + gB1 = 180 độ

=> gB1 = 180 - gA1 = 180 - 100= 80 độ

Ta có gB1 = gB3 = 80 độ ( hai góc đối đỉnh)

ta có : a \(\perp\) P và b \(\perp\) Q \(\Rightarrow\)a//b

 M1 và N1 là cặp góc trong cùng phía bù nhau 

    \(\Rightarrow\)M1= \(^{180^0}\)- N1= 180- \(65^0\)= 115

a) \(\overrightarrow {MN}  = 3\overrightarrow a \)có độ dài bằng 3 lần vectơ \(\overrightarrow a \), cùng hướng với vectơ \(\overrightarrow a \)

Suy ra, từ điểm M vẽ vectơ MN với độ dài là 6 ô vuông và có hướng từ trái sang phải

\(\overrightarrow {MP}  =  - 3\overrightarrow b \)có độ dài bằng 3 lần vectơ \( - \overrightarrow b \), ngược hướng với vectơ \(\overrightarrow b \)

Suy ra, từ điểm M vẽ vectơ MP với độ dài là 3 đường chéo ô vuông và có hướng từ trên xuống dưới chếch sang trái

b) Hình vuông với cạnh bằng 1 thì ta tính được đường chéo có độ dài là \(\sqrt 2 \); \(\left| {\overrightarrow b } \right| = \sqrt 2 \) . Suy ra:

\(\left| {3\overrightarrow b } \right| = 3\left| {\overrightarrow b } \right| = 3\sqrt 2 \); \(\left| { - 3\overrightarrow b } \right| = 3\left| {\overrightarrow { - b} } \right| = 3\sqrt 2 \); \(\left| {2\overrightarrow a  + 2\overrightarrow b } \right| = \left| {2\left( {\overrightarrow a  + \overrightarrow b } \right)} \right| = 2\left| {\overrightarrow a  + \overrightarrow b } \right|\)

Từ điểm cuối của vectơ \(\overrightarrow a \) vẽ một vectơ bằng vectơ \(\overrightarrow b \) ta có \(\overrightarrow c  = \overrightarrow a  + \overrightarrow b \)

Áp dụng định lý cosin ta tính được độ dài của vectơ \(\overrightarrow c \)là \(\left| {\overrightarrow c } \right| = \sqrt {{{\left| {\overrightarrow a } \right|}^2} + {{\left| {\overrightarrow b } \right|}^2} - 2\left| {\overrightarrow a } \right|\left| {\overrightarrow b } \right|\cos \left( {\widehat {\overrightarrow a ,\overrightarrow b }} \right)}  = \sqrt {{2^2} + {{\sqrt 2 }^2} - 2.2.\sqrt 2 .\cos \left( {135^\circ } \right)}  = \sqrt {10} \)

\( \Rightarrow \left| {2\overrightarrow a  + 2\overrightarrow b } \right| = 2\left| {\overrightarrow a  + \overrightarrow b } \right| = 2\left| {\overrightarrow c } \right| = 2\sqrt {10} \)

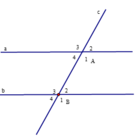
+) Vì   a // b nên  A ^ 1 + B ^ 2 = 180 ∘  (cặp góc trong cùng phía)

Mặt khác  A ^ 1 − B ^ 2 = 70 0

⇒ A ^ 1 = 180 ∘ + 70 ∘ : 2 = 125 ∘ và  B ^ 2 = 180 ∘ − 125 ∘ = 55 ∘

+) Ta có A ^ 3 = A ^ 1 (hai góc đối đỉnh) mà  A ^ 1 = 125 ∘

⇒ A ^ 3 = 125 ∘

Ta có B ^ 2 = B ^ 4  (hai góc đối đỉnh) mà  B ^ 2 = 55 ∘

⇒ B ^ 4 = 55 ∘

a: m⊥AB

n⊥AB

Do đó: m//n

Hình đâu em nhỉ, không có hình thì cô chịu nhé

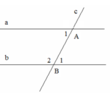
Ta có: B ^ 1 + B ^ 2 = 180 0 . ( Kề bù), mà  B ^ 1 = 1 2 B ^ 2  nªn  B ^ 1 = 180 0 : 3 = 60 0

⇒ A ^ 1 = B ^ 1 = 60 0

Do đó a//b ( vì có cặp góc so le trong bằng nhau).

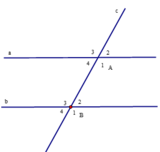
a) Vì B 2 ^ , A 1 ^  là cặp góc trong cùng phía nên ta có:

B 2 ^ + A 1 ^ = 180 0 ⇒ A 1 ^ = 180 0 − B 2 ^ = 180 0 − 45 0 = 135 0 .

b) Ta có B ^ 1 = A ^ 1 = 135 ∘  (hai góc đồng vị)

mà A ^ 3 = A ^ 1 = 135 ∘  (hai góc đối đỉnh)

Vậy  B ^ 1 = A ^ 3 = 135 ∘

c) Ta có A ^ 1 + A ^ 2 = 180 ∘ (hai góc kề bù) mà B ^ 1 = A ^ 1  (theo câu b)

Do đó  A ^ 2 + B ^ 1 = 180 ∘