Cho tứ diện SABC có tam giác ABC vuông tại B, AB = a , BC = a 3 và SA = a 2 , SB = a 2 , SC = a 5 . Tính bán kính mặt cầu ngoại tiếp tứ diện S.ABC.
A. R = a 37 28
B. R = a 259 7
C. R = a 259 14
D. R = a 37 14
Những câu hỏi liên quan
Cho hình tứ diện SABC có đáy ABC là tam giác vuông tại B, có AB = a, BC =a\(\sqrt{5}\), SA vuông góc với (ABC), SA = a\(\sqrt{6}\)
a) Tính (SB;(ABC))
b) Tính (SA;(SBC))
a: (SB;(ABC))=(SB;BA)=góc SBA
\(\tan SBA=\dfrac{SA}{AB}=\sqrt{6}\)
=>góc SBA=68 độ
b: (SA;(SBC))=(SA;SB)=góc ASB
tan ASB=AB/SA=1/căn 6
=>góc ASB=22 độ
Đúng 0
Bình luận (0)
Cho tứ diện SABC có ABC là tam giác vuông cân tại A, đường cao SA. Biết đường cao AH của tam giác ABC bằng a, góc giữa mặt phẳng (SBC) và mặt phẳng (ABC) bằng
60
0
.Tính theo a thể tích khối tứ diện SABC
A
.
a
3
6
3
B
.
a...
Đọc tiếp
Cho tứ diện SABC có ABC là tam giác vuông cân tại A, đường cao SA. Biết đường cao AH của tam giác ABC bằng a, góc giữa mặt phẳng (SBC) và mặt phẳng (ABC) bằng 60 0 .Tính theo a thể tích khối tứ diện SABC
A . a 3 6 3
B . a 3 3 3
C . 2 a 3 6 3
D . a 3 2 3
Cho tứ diện SABC. Tam giác ABC vuông tại B. SA vuông góc mặt phẳng ABC. Gọi A, AK lần lượt là đường cao tam giác SAB, SAC. Đường thẳng HK cắt BC tại I. Chứng minh: tam giác IAC vuông
Xem chi tiết
Cho tứ diện SABC có SA vuông góc với mặt phẳng (ABC) và tam giác ABC vuông tại B. Trong mp(SAB), kẻ AM vuông góc với SB tại M. Trên cạnh SC lấy điểm N sao cho SM/SB = SN/SC .
Chứng minh rằng:
a) BC ⊥ (SAB), AM ⊥ (SBC)
b) SB ⊥ AN
Cho tứ diện SABCD có ABC là tam giác vuông cân tại A, đường cao SA Biết đường cao AH của tam giác ABC bằng a, góc giữa mặt phẳng (SBC) và mặt phẳng (ABC) bằng
60
°
.Tính theo a thể tích khối tứ diện SABC A.
a
3
6
3
B.
a
3
3
3...
Đọc tiếp
Cho tứ diện SABCD có ABC là tam giác vuông cân tại A, đường cao SA Biết đường cao AH của tam giác ABC bằng a, góc giữa mặt phẳng (SBC) và mặt phẳng (ABC) bằng 60 ° .Tính theo a thể tích khối tứ diện SABC
A. a 3 6 3
B. a 3 3 3
C. 2 a 3 6 3
D. a 3 2 3
Cho hình chóp SABC có đáy là tam giác ABC vuông tại B. SA vuông góc với(ABC), AB = a, AC = 3a, SA = 2a.
a. chứng minh BC vuông góc (ABC).
b. Tính thể tích khối chóp SABC.
6 tháng 7 2021 lúc 21:17
cho hình chóp SABC có SA=a, SA vuông góc với (ABC). Tam giác ABC vuông cân tại B và AB=a, kẻ AH vuông góc với SC tại H. VSABH là
\(\dfrac{V_{SABH}}{V_{SABC}}=\dfrac{SH}{SC}=\left(\dfrac{SA}{SC}\right)^2\Rightarrow V_{SABN}=\left(\dfrac{SA}{SC}\right)^2.V_{SABC}\)
\(AC^2=AB^2+BC^2=2AB^2=2a^2\)
\(SC=\sqrt{SA^2+AC^2}=\sqrt{a^2+2a^2}=a\sqrt{3}\)
\(\Rightarrow V_{SABH}=\left(\dfrac{a}{a\sqrt{3}}\right)^2.\dfrac{1}{3}.SA.AB^2=\dfrac{a^3}{9}\)
Đúng 2
Bình luận (0)
Bài 17: Cho hình chóp SABC có đáy ABC là tam giác đều cạnh a, SA = 3a và SA vuông góc với đáy. Gọi H và I lần lượt là trực tâm tam giác ABC và SBC.
a) Chứng minh rằng IH vuông (SBC).
b) Tính thể tích khối tứ diện IHBC theo a
Ta có: \(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp BH\\BH\perp AC\left(\text{H là trực tâm ABC}\right)\end{matrix}\right.\) \(\Rightarrow BH\perp\left(SAC\right)\Rightarrow BH\perp SC\) (1)
Lại có I là trực tâm SBC \(\Rightarrow BI\perp SC\) (2)
(1);(2) \(\Rightarrow SC\perp\left(BIH\right)\Rightarrow SC\perp IH\) (3)
Gọi M là giao điểm AH và BC \(\Rightarrow\) M là trung điểm BC (do tam giác ABC đều)
Mà SBC cân tại S (dễ dàng chứng minh SB=SC bằng Pitago) \(\Rightarrow SM\) đồng thời là đường cao trong tam giác SBC hay \(I\in SM\)
\(\Rightarrow IH\in\left(SAM\right)\)
\(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp BC\\AH\perp BC\left(\text{H là trực tâm ABC}\right)\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAM\right)\Rightarrow BC\perp IH\) (4)
(3); (4) \(\Rightarrow IH\perp\left(SBC\right)\)
b.
\(AM=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều) \(\Rightarrow SM=\sqrt{SA^2+AM^2}=\dfrac{a\sqrt{39}}{2}\)
ABC đều nên H là trực tâm đồng thời là trọng tâm \(\Rightarrow\dfrac{MH}{AM}=\dfrac{1}{3}\) \(\Rightarrow MH=\dfrac{AM}{3}=\dfrac{a\sqrt{3}}{6}\)
\(\Rightarrow IM=MH.cos\widehat{AMS}=MH.\dfrac{AM}{SM}=\dfrac{a\sqrt{39}}{78}\)
\(V_{IHBC}=\dfrac{IM}{SM}.\dfrac{MH}{AM}.V_{SABC}=\dfrac{1}{117}.\dfrac{1}{3}.3a.\dfrac{a^2\sqrt{3}}{4}=\dfrac{a^3\sqrt{3}}{468}\)
Đúng 0
Bình luận (0)
Cho tứ diện SABC có SA vuông góc với mặt phẳng (ABC), SA SB 3 cm, BC 5cm và diện tích tam giác SAC bằng 6
c
m
2
. Một mặt phẳng
α
thay đổi qua trọng tâm G của tứ diện cắt các cạnh AS, AB, AC lần lượt tại M, N, P. Tính giá trị nhỏ nhất
T
m
của biểu thức
T
1...
Đọc tiếp
Cho tứ diện SABC có SA vuông góc với mặt phẳng (ABC), SA= SB= 3 cm, BC =5cm và diện tích tam giác SAC bằng 6 c m 2 . Một mặt phẳng α thay đổi qua trọng tâm G của tứ diện cắt các cạnh AS, AB, AC lần lượt tại M, N, P. Tính giá trị nhỏ nhất T m của biểu thức T = 1 A M 2 + 1 A N 2 + 1 A P 2
A. T m = 8 17
B. T m = 41 144
C. T m = 1 10
D. T m = 1 34
Chọn A
Vì tam giác SAC vuông tại A
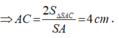
nên tam giác ABC vuông tại A. Chọn hệ trục Oxyz như hình vẽ
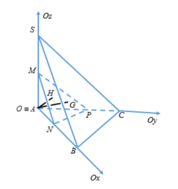
Ta có
A(0;0;0), B(3;0;0), C(0;4;0), S(0;0;3)
Vì G là trọng tâm của tứ diện SABC nên ta có
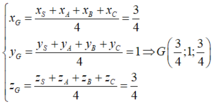
Gọi H là hình chiếu của điểm A lên mặt phẳng α . Theo tính chất của tam diện vuông ta có
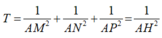
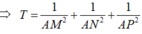
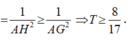
Dấu “=” xảy ra khi H ≡ G tức mặt phẳng α đi qua điểm G và vuông góc với đường thẳng OG.
Vậy giá trị nhỏ nhất của T bằng 8 17
Đúng 0
Bình luận (0)