Các câu hỏi tương tự
Cho hình lăng trụ tam giác ABC.ABC có BBa, góc giữa đường thẳng BB và mặt phẳng (ABC) bằng
60
0
, tam giác ABC vuông tại C và
B
A
C
^
60
0
. Hình chiếu vuông góc của điểm B lên mặt phẳng (ABC) trùng với trọng tâm tam giác ABC. Thể tích của khối tứ diện A.ABC tính theo a bằng A.
9...
Đọc tiếp
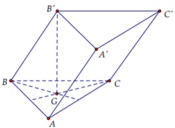
Cho hình lăng trụ tam giác ABC.A'B'C' có BB'=a, góc giữa đường thẳng BB' và mặt phẳng (ABC) bằng 60 0 , tam giác ABC vuông tại C và B A C ^ = 60 0 . Hình chiếu vuông góc của điểm B' lên mặt phẳng (ABC) trùng với trọng tâm tam giác ABC. Thể tích của khối tứ diện A'.ABC tính theo a bằng
A. 9 a 3 416 .
B. 13 a 3 108 .
C. 9 a 3 208 .
D. 13 a 3 416 .
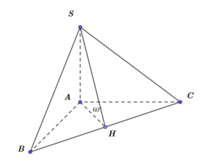
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, SA vuông góc với đáy, khoảng cách từ A đến mặt phẳng (SBC) bằng 3. Gọi
α
là góc giữa hai mặt phẳng (SBC) và (ABC), tính
cos
α
khi thể tích khối chóp
S
.
A
B
C
nhỏ nhất. A.
cos
α
2
2
B.
cos
α
1
3...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, SA vuông góc với đáy, khoảng cách từ A đến mặt phẳng (SBC) bằng 3. Gọi α là góc giữa hai mặt phẳng (SBC) và (ABC), tính cos α khi thể tích khối chóp S . A B C nhỏ nhất.
A. cos α = 2 2
B. cos α = 1 3
C. cos α = 3 3
D. cos α = 2 3
Cho tứ diện S.ABC có các tam giác SAB, SAC và ABC vuông cân tại A,
S
A
a
. Gọi
α
là góc giữa hai mặt phẳng
S
B
C
và
A
B
C
bằng A.
3
B.
1
2
C.
2
D. ...
Đọc tiếp
Cho tứ diện S.ABC có các tam giác SAB, SAC và ABC vuông cân tại A, S A = a . Gọi α là góc giữa hai mặt phẳng S B C và A B C bằng
A. 3
B. 1 2
C. 2
D. 1 3
Cho hình chóp SABC có đáy là tam giác đều cạnh a, SA vuông góc với mặt phẳng đáy, góc giữa hai mặt phẳng (SBC) và (ABC) bằng
60
°
. Tính thể tích V của khối chóp SABC A.
V
a
3
3
8
B.
V
a
3
12
C.
V...
Đọc tiếp
Cho hình chóp SABC có đáy là tam giác đều cạnh a, SA vuông góc với mặt phẳng đáy, góc giữa hai mặt phẳng (SBC) và (ABC) bằng 60 ° . Tính thể tích V của khối chóp SABC
A. V = a 3 3 8
B. V = a 3 12
C. V = a 3 3 4
D. V = a 3 3 12
Cho hình chóp S.ABC có đáy là tam giác vuông cân ở A, cạnh BC2
3
a. Tam giác SBC cân tại S và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Biết thể tích khối chóp là
a
3
, tính góc giữa SA và mặt phẳng (SBC). A.
π
/6 B.
π
/3 C.
π
/4 D. arctan
3
2
Đọc tiếp
Cho hình chóp S.ABC có đáy là tam giác vuông cân ở A, cạnh BC=2 3 a. Tam giác SBC cân tại S và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Biết thể tích khối chóp là a 3 , tính góc giữa SA và mặt phẳng (SBC).
A. π /6
B. π /3
C. π /4
D. arctan 3 2
Cho hình chóp SABC có đáy là tam giác đều cạnh a, SA vuông góc với mặt phẳng đáy, góc giữa hai mặt phẳng (SBC) và (ABC) bằng
60
°
. Thể tích của khối chóp SABC bằng A.
a
3
3
8
B.
a
3
12
C.
a
3...
Đọc tiếp
Cho hình chóp SABC có đáy là tam giác đều cạnh a, SA vuông góc với mặt phẳng đáy, góc giữa hai mặt phẳng (SBC) và (ABC) bằng 60 ° . Thể tích của khối chóp SABC bằng
A. a 3 3 8
B. a 3 12
C. a 3 3 4
D. a 3 3 12
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB = 3, BC = 4, đường thẳng SA vuông góc với mặt phẳng (ABC), SA = 4. Gọi AM, AN lần lượt là chiều cao của tam giác SAB và SAC. Thể tích khối tứ diện AMNC là
A. 128/41
B. 768/41
C. 384/41
D. 256/41
Cho hình lăng trụ ABC ABC có AAa, góc giữa cạnh bên và mặt đáy bằng 60°. Tam giác ABC vuông tại C và góc
B
A
C
^
60
°
. Hình chiếu vuông góc của B lên mặt phẳng
A
B
C
trùng với trọng tâm của
Δ
A
B
C
. Tính thể tích khối tứ diện AABC theo a A....
Đọc tiếp
Cho hình lăng trụ ABC A'B'C' có AA'=a, góc giữa cạnh bên và mặt đáy bằng 60°. Tam giác ABC vuông tại C và góc B A C ^ = 60 ° . Hình chiếu vuông góc của B' lên mặt phẳng A B C trùng với trọng tâm của Δ A B C . Tính thể tích khối tứ diện A'ABC theo a
A. V A ' A B C = 3 a 3 208
B. V A ' A B C = 27 a 3 208
C. V A ' A B C = 81 a 3 208
D. V A ' A B C = 9 a 3 208
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB 3, BC 4, đường thẳng SA vuông góc với mặt phẳng (ABC), SA 4. Gọi AM, AN lần lượt là chiều cao các tam giác SAB và SAC. Thể tích khối tứ diện AMNC là A.
128
41
.
B.
256
41
.
C.
768
41
.
D. ...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB = 3, BC = 4, đường thẳng SA vuông góc với mặt phẳng (ABC), SA = 4. Gọi AM, AN lần lượt là chiều cao các tam giác SAB và SAC. Thể tích khối tứ diện AMNC là
A. 128 41 .
B. 256 41 .
C. 768 41 .
D. 384 41