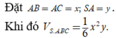
Vì AB, AC, AS đôi một vuông góc nên
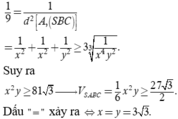
![]()
Chọn C.

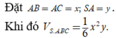
Vì AB, AC, AS đôi một vuông góc nên
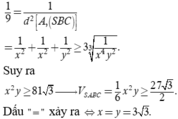
![]()
Chọn C.
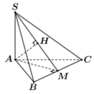
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại C ; SA vuông góc với đáy; SC = a. Gọi α là góc giữa hai mặt phẳng (SBC) và (ABC). Tính sin α để thể tích khối chóp S.ABC lớn nhất
A. sin α = 1 3
B. sin α = 1 3
C. sin α = 2 3
D. sin α = 6 3
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, AB=2a, SA vuông góc với mặt đáy và góc giữa SB mặt đáy bằng 60 ° . Gọi α là góc giữa hai mặt phẳng (SBC) và (ABC). Giá trị cosα bằng
A. 15 5
B. 1 7
C. 2 5
D. 2 7
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, hình chiếu vuông góc của đỉnh S xuống mặt đáy nằm trong hình vuông ABCD. Hai mặt phẳng (SAD), (SBC) vuông góc với nhau; góc giữa hai mặt phẳng S A B v à S A C là 60 ° ; góc giữa hai mặt phẳng S A B v à S A D là 45 ° Gọi α là góc giữa hai mặt phẳng S A B v à A B C D , tính cos α
A. cos α = 1 2
B. cos α = 2 2
C. cos α = 3 2
D. cos α = 2 3
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB=a, BC=2a, cạnh bên SA vuông góc với mặt đáy (ABC) và SA=3a. Gọi α là góc giữa hai mặt phẳng (SAC) và (SBC). Tính sin.
A. sin α = 1 3
B. sin α = 4138 120
C. sin α = 13 7
D. sin α = 7 5
Cho lăng trụ đứng ABC.A’B’C’ có đáy là tam giác vuông tại B, AB = a, BC = 2a. Biết thể tích của khối lăng trụ ABC.A’B’C’ bằng 2 2 a 3 . Gọi α là góc giữa mặt phẳng (A’BC) với mặt phẳng (ABC). Khi đó cos của góc α bằng:
![]()
![]()
![]()
![]()
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, A B = 1 , B C = 3 mặt bên SAC là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi α là số đo của góc giữa hai mặt phẳng (SAB) và (SBC). Khi đó cos α bằng
A. 65 65
B. 65 10
C. 65 20
D. 2 65 65
Cho hình chóp S.ABC có SC = 2a và SC ⊥ (ABC). Đáy ABC là tam giác vuông cân tại B và có AB = a l 2 . Mặt phẳng ( α ) đi qua C và vuông góc với SA, ( α ) cắt SA, SB lẩn lượt tại D, E. Tính thể tích khối chóp S.CDE.
A. 4 a 3 9
B. 2 a 3 3
C. 2 a 3 9
D. a 3 3
Hình chóp S.ABC có đáy là tam giác vuông tại B có AB=a, AC=2a, SA vuông góc với mặt phẳng đáy, SA=2a. Gọi α là góc tạo bởi hai mặt phẳng (SAC) và (SBC). Tính cosα .
A. 15 5
B. 3 5
C. 1 2
D. 3 2
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, cạnh bên SA vuông góc với đáy. Biết rằng khoảng cách từ điểm A đến mặt phẳng (SBC) bằng a. Xét góc α thảy đổi là số đo của góc giữa đường thẳng SB và mặt phẳng đáy. Tính cos α sao cho thể tích của hình chóp S.ABCD đạt giá trị nhỏ nhất
A. cos α = 3 6
B. cos α = 6 3
C. cos α = 3 3
D. cos α = 6 6