Cho ba mặt phẳng (α), (β), (γ), những mệnh đề nào sau đây đúng?
a) Nếu (α) ⊥ (β) và (α) // (γ) thì (β) ⊥ (γ).
b) Nếu (α) ⊥ (β) và (α) ⊥ (γ) thì (β) // (γ).
a) Đúng.
(α) ⊥ (β) ⇒ ∃ đường thẳng d ⊂ (β) và d ⊥ (α ).
Mà (α ) // (γ)
⇒ d ⊥ (γ)
⇒ (β) ⊥ (γ).
b) Sai, vì hai mặt phẳng (β), (γ) cùng vuông góc với mp(α) có thể song song hoặc cắt nhau.
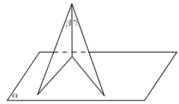
Chứng minh rằng các biểu thức sau là những hằng số không phụ thuộc α, β
[ tan ( 90 ο - α ) - c o t ( 90 ο + α ) ] 2 - [ c o t ( 180 ο + α ) + c o t ( 270 ο + α ) ] 2
Đặt α = log 2 , β = log 3 , γ = log 7 . Hãy biểu diễn log 2016 theo α , β v à γ
A. log 2016 = 2 α - 5 β - γ
B. log 2016 = 5 α - 2 β - γ
C. log 2016 = 5 α + 2 β + γ
D. log 2016 = 10 α β γ
Cho 0<a,b,c,x ≢ 1 . Biết log a x = α , log b x = β , log c x = γ , tính log a b c x theo α , β , γ .
A. log a b c x = α + β + γ
B. log a b c x = α β γ
C. log a b c x = α β + β γ + γ α α β γ
D. log a b c x = α β γ α β + β γ + γ α
Cho 0 < a , b , c , x ≠ 1 ; a b c ≠ 1 . Biết log a x = α , log b x = β , log c x = γ , tính log a b c x theo α , β , γ .
A. log a b c x = α + β + γ
B. log a b c x = α β γ
C. log a b c x = α β + β γ + γ α α β γ
D. log a b c x = α β γ α β + β γ + γ α
Đáp án D.
Ta có log x a = 1 α ; log x b = 1 β ; log x c = 1 γ
⇒ log x a + log x b + log x c = 1 α + 1 β + 1 γ ⇒ log x a b c = α β + β γ + γ α α β γ
⇔ log a b c x = α β γ α β + β γ + γ α .
CMR nếu α+β=90 độ thì sin α =cosβ, tan α= cot β
\(sin\alpha=cos\beta=\dfrac{AB}{BC}\)
\(tan\alpha=cot\beta=\dfrac{AB}{AC}\)
\(\alpha+\beta=90^o\)
\(\Rightarrow\beta=90^o-\alpha\)
Theo đề bài :
\(sin\alpha=cos\beta\)
\(\Rightarrow sin\alpha=cos\left(90^o-\alpha\right)\)
mà \(\alpha;90^o-\alpha\) là 2 góc phụ nhau
\(\Rightarrow cos\left(90^o-\alpha\right)=sin\alpha\left(dpcm\right)\)
Tương tự \(tan\alpha=cot\beta=cot\left(90^o-\alpha\right)\)
Cho α + β + γ = π . Khi đó
A. s i n α + β = sin γ
B. cos α + β = cos γ
C. tan α + β = t a n γ
D. c o t α + β = c o t γ
α + β và γ là hai góc (cung) bù nhau nên A đúng.
Cho α + β + γ = π . Khi đó
A. cos α + β 2 = cos γ 2
B. cos α + β 2 = sin γ 2
C. cos α + β 2 = - cos γ 2
D. cos α + β 2 = - sin γ 2
Ta có: α + β + γ = π ⇒ α + β = π - γ ⇒ α + β 2 = π 2 - γ 2
α + β 2 và γ 2 là hai góc (cung) phụ nhau nên B đúng và A, C, D sai.
Cho α + β + γ = π . Khi đó
A. tan 2 α + 2 β = tan 2 γ
B. c o t 2 α + 2 β = c o t 2 γ
C. sin 2 α + 2 β = sin 2 γ
D. cos 2 α + 2 β = cos 2 γ
Ta có: α + β + γ = π . Suy ra:
2 α + 2 β = - 2 γ + 2 π nên cos 2 α + 2 β = cos - 2 γ = cos 2 γ
nhưng sin 2 α + 2 β = sin - 2 γ = - sin 2 γ .
Từ đó D đúng và A, B, C sai.
