Công bội nguyên dương của cấp số nhân ( u n ) thoả mãn :
u 1 + u 2 + u 3 = 14 u 1 u 2 u 3 = 64 l à :
A. 3
B. 2
C. 1
D. 0
Công bội nguyên dương của cấp số nhân ( u n ) thoả mãn :
u 1 + u 2 + u 3 = 21 1 u 1 + 1 u 2 + 1 u 3 = 7 12 l à
A. 3
B. 2
C. 1
D. 0
Chọn B
Ta giải hệ:
u 1 q 2 + q + 1 = 21 1 u 1 1 + 1 q + 1 q 2 = 7 12
⇔ q 2 + q + 1 21 = 1 u 1 1 u 1 q 2 + q + 1 q 2 = 7 12 ⇔ q 2 + q + 1 21 = 1 u 1 q 2 + q + 1 21 . q 2 + q + 1 q 2 = 7 12 *
Giải (*)
( q 2 + q + 1 ) 2 q 2 = 49 4 ⇔ q 2 + q + 1 q = ± 7 2
TH1: q 2 + q + 1 q = 7 2 ⇔ q = 2 q = 1 2 ( l o a i )
TH2; q 2 + q + 1 q = − 7 2 ⇔ q = − 9 + 65 4 q = − 9 − 65 4 ( l o a i )
Vậy q=2
cho cấp số cộng (u\(_n\)) có công sai d khác 0 và cấp số nhân (v\(_n\)) có công bội q là số dương thỏa mãn \(u_1=v_1=-2\); \(u_2=v_2\); \(u_3=v_3+8\). tính tổng d+q
\(u_2=u_1+d=-2+d\) ; \(v_2=v_1q=-2q\)
\(u_2=v_2\Rightarrow-2+d=-2q\Rightarrow d=2-2q\)
\(u_3=v_3+8\Leftrightarrow-2+2d=-2q^2+8\)
\(\Leftrightarrow-2+2\left(2-2q\right)=-2q^2+8\)
\(\Leftrightarrow2q^2-4q-6=0\Rightarrow\left[{}\begin{matrix}q=-1\Rightarrow d=4\\q=3\Rightarrow d=-4\end{matrix}\right.\)
a. Có nhận xét gì về công bội của các cấp số nhân lùi vô hạn?
b. Cho ví dụ về một cấp số nhân lùi vô hạn và có công bội là số âm và một cấp số nhân lùi vô hạn có công bội là số dương và tính tổng của các cấp số nhân đó.
a) Cấp số nhân vô hạn với công bội q mà |q| < 1 là cấp số nhân lùi vô hạn
b) Ví dụ về cấp số nhân lùi vô hạn có công bội âm:
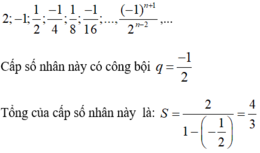

a) Có nhận xét gì về công bội của các cấp số nhân lùi vô hạn ?
b) Cho ví dụ về một cấp số nhân lùi vô hạn có công bội là số âm và một cấp số nhân lùi vô hạn có công bội là số dương và tính tổng của mỗi cấp số nhân đó ?
Cho số nguyên dương n thoả mãn C n 1 ; C n 2 ; C n 3 lần lượt là số hạng thứ nhất, thứ 5 và thứ 15 của một cấp số cộng. Giá trị của n bằng
![]()
![]()
![]()
![]()
Cho số nguyên dương n thoả mãn C n 1 , C n 2 , C n 3 lần lượt là số hạng thứ nhất, thứ 5 và thứ 15 của một cấp số cộng. Giá trị của n bằng
A. 9
B. 10
C. 11
D. 12
Cho cấp số nhân u n thỏa mãn điều kiện u n > 0 u 6 = 16 u 2 . Khi đó công bội q của cấp số nhân bằng
A. 4
B. 2
C. 2
D. -2
Một cấp số nhân dương có 4 số hạng, công bội q bằng 1/4 lần số hạng thứ nhất, tổng của hai số hạng đầu bằng 24. Tìm tích các số hạng cấp số nhân đó?
A. 2
B. 1
C. 4096
D. 262144
Cho tập A = {1, 2, 3, ..., 2018}. Có bao nhiêu cách chọn ra 5 số từ tập A mà các số đó lập thành một cấp số nhân tăng có công bội là một số nguyên dương ?
A. 126
B. 161
C. 166
D. 31
Năm số được chọn ra xếp được duy nhất dãy tăng, giả sử là
x 1 < x 2 < x 3 < x 4 < x 5
Theo giả thiết các số đó là x 1 , q x 1 , q 2 x 1 , q 3 x 1 , q 4 x 1 và q ∈ ℕ , q ≥ 2
Vì ![]()
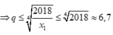
![]()
Mặt khác
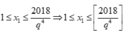
Vậy với mỗi số nguyên q thuộc tập X={ 2;3;4;5;6}
ta có 2018 q 4 cách chọn x1 các số x2, x3, x4, x5 có tương ứng duy nhất một cách chọn.
Vậy theo quy tắc cộng và quy tắc nhân có tất cả
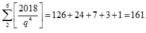
Chọn đáp án B.