Tính I = ∫ 0 1 e 3 x d x
![]()
![]()
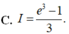
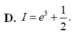
( Mu4-42. Cho hàm so $f(x)$ có đạo hàm trên đoạn $[0 ; 1]$ thỏa mãn $f(1)=0$ và $\int_0^1\left[f^{\prime}(x)\right]^2 d x=\int_0^1(x+1) e^x f(x) d x=\frac{e^2-1}{4}$. Tinh tich phân $I=\int_{0}^1 f(x) d x$.
A. $I=2-e$.
B. $I=\frac{e}{2}$.
C. $l=e-2$.
D. $1=\frac{e-1}{2}$
I) THỰC HIỆN PHÉP TÍNH a) 2x(x^2-4y) b)3x^2(x+3y) c) -1/2x^2(x-3) d) (x+6)(2x-7)+x e) (x-5)(2x+3)+x II phân tích đa thức thành nhân tử a) 6x^2+3xy b) 8x^2-10xy c) 3x(x-1)-y(1-x) d) x^2-2xy+y^2-64 e) 2x^2+3x-5 f) 16x-5x^2-3 g) x^2-5x-6 IIITÌM X BIẾT a)2x+1=0 b) -3x-5=0 c) -6x+7=0 d)(x+6)(2x+1)=0 e)2x^2+7x+3=0 f) (2x-3)(2x+1)=0 g) 2x(x-5)-x(3+2x)=26 h) 5x(x-1)=x-1 IV TÌM GTNN,GTLN. a) tìm giá trị nhỏ nhất x^2-6x+10 2x^2-6x b) tìm giá trị lớn nhất 4x-x^2-5 4x-x^2+3
Giải như sau.
(1)+(2)⇔x2−2x+1+√x2−2x+5=y2+√y2+4⇔(x2−2x+5)+√x2−2x+5=y2+4+√y2+4⇔√y2+4=√x2−2x+5⇒x=3y(1)+(2)⇔x2−2x+1+x2−2x+5=y2+y2+4⇔(x2−2x+5)+x2−2x+5=y2+4+y2+4⇔y2+4=x2−2x+5⇒x=3y
⇔√y2+4=√x2−2x+5⇔y2+4=x2−2x+5, chỗ này do hàm số f(x)=t2+tf(x)=t2+t đồng biến ∀t≥0∀t≥0
Công việc còn lại là của bạn !
\(\left(x+6\right)\left(2x+1\right)=0\)
<=> \(\orbr{\begin{cases}x+6=0\\2x+1=0\end{cases}}\)
<=> \(\orbr{\begin{cases}x=-6\\x=-\frac{1}{2}\end{cases}}\)
Vậy....
hk tốt
^^
Cho E = \(\left(\frac{x+1}{x-1}-\frac{x-1}{x+1}\right)\) : \(\left(\frac{1}{x+1}-\frac{x}{1-x}+\frac{2}{x^2-2}\right)\)
a. Rút gọn E
b. Tính E khi x² - 9 = 0
c. Tìm giá trị của x để E = 3
d. Tìm x để E<0
e. Tính x khi E - x - 3 = 0
Mọi người giúp em với ạ. Xin cảm ơn.
Bài 1:cho biểu thức D=\(\left(\frac{1}{1-x}+\frac{1}{1+x}\right):\left(\frac{1}{1-x}-\frac{1}{1+x}\right)+\frac{1}{x+1}\)
a) Rút gọn D. b) Tính giá trị của D khi \(x^2-x=0\) C) Tìm giá trị của x khi D=3/2.
Bài 2: Cho biểu thức. E=\(\left(\frac{x+1}{x-1}-\frac{x-1}{x+1}\right):\left(\frac{1}{x+1}-\frac{x}{1-x}+\frac{2}{x^2-2}\right)\)
a) Rút gọn E. b) Tính E khi \(x^2-9=0\) c)Tìm giá trị của x để E=-3. d)Tìm x để E<0. e) Tính x khi E-x-3=0
Bài 1:
a) đkxđ: \(x\ne0;x\ne\pm1\)
\(D=\left(\frac{1}{1-x}+\frac{1}{1+x}\right)\div\left(\frac{1}{1-x}-\frac{1}{1+x}\right)+\frac{1}{x+1}\)
\(D=\left[\frac{1+x+1-x}{\left(1-x\right)\left(1+x\right)}\right]\div\left[\frac{1+x-1+x}{\left(1-x\right)\left(1+x\right)}\right]+\frac{1}{x+1}\)
\(D=\frac{2}{\left(1-x\right)\left(1+x\right)}\div\frac{2x}{\left(1-x\right)\left(1+x\right)}+\frac{1}{x+1}\)
\(B=\frac{1}{x}+\frac{1}{x+1}\)
\(B=\frac{2x+1}{x+1}\)
b) Ta có: \(x^2-x=0\Leftrightarrow x\left(x-1\right)=0\Leftrightarrow\orbr{\begin{cases}x=0\\x-1=0\end{cases}}\Rightarrow\orbr{\begin{cases}x=0\\x=1\end{cases}}\) đều ko thỏa mãn đkxđ
c) Khi \(D=\frac{3}{2}\)
\(\Leftrightarrow\frac{2x+1}{x+1}=\frac{3}{2}\)
\(\Leftrightarrow4x+2=3x+3\Rightarrow x=1\) không thỏa mãn đkxđ
Bài 2: (Sửa đề tí nếu sai ib t lm lại nhé:)
a) đkxđ: \(x\ne\pm1\)
\(E=\left(\frac{x+1}{x-1}-\frac{x-1}{x+1}\right)\div\left(\frac{1}{x+1}-\frac{x}{1-x}+\frac{2}{x^2-1}\right)\)
\(E=\frac{\left(x+1\right)^2-\left(x-1\right)^2}{\left(x-1\right)\left(x+1\right)}\div\frac{x-1+x\left(x+1\right)+2}{\left(x-1\right)\left(x+1\right)}\)
\(E=\frac{x^2+2x+1-x^2+2x-1}{x-1+x^2+x+2}\)
\(E=\frac{4x}{\left(x+1\right)^2}\)
b) Ta có: \(x^2-9=0\Rightarrow\orbr{\begin{cases}x=3\\x=-3\end{cases}}\)
+ Nếu: \(x=3\)
=> \(E=\frac{4.3}{\left(3+1\right)^2}=\frac{3}{4}\)
+ Nếu: \(x=-3\)
=> \(E=\frac{4.\left(-3\right)}{\left(-3+1\right)^2}=-3\)
c) Để \(E=-3\)
\(\Leftrightarrow\frac{4x}{\left(x+1\right)^2}=-3\)
\(\Leftrightarrow4x=-3x^2-6x-3\)
\(\Leftrightarrow3x^2+10x+3=0\)
\(\Leftrightarrow\left(x+3\right)\left(3x+1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x+3=0\\3x+1=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=-3\\x=-\frac{1}{3}\end{cases}}\)
d) Để \(E< 0\)
\(\Leftrightarrow\frac{4x}{\left(x+1\right)^2}< 0\) , mà \(\left(x+1\right)^2>0\left(\forall x\right)\)
=> Để E < 0 => \(4x< 0\Rightarrow x< 0\)
Vậy x < 0 thì E < 0
e) Ta có: \(E-x-3=0\)
\(\Leftrightarrow\frac{4x}{\left(x+1\right)^2}=x+3\)
\(\Leftrightarrow4x=\left(x^2+2x+1\right)\left(x+3\right)\)
\(\Leftrightarrow x^3+5x^2+7x+3-4x=0\)
\(\Leftrightarrow x^3+5x^2+3x+3=0\)
Đến đây bấm máy tính thôi, nghiệm k đc đẹp cho lắm:
\(x=-4,4798...\) ; \(x=-0,2600...+0,7759...\) ; \(x=-0,2600...-0,7759...\)
I) THỰC HIỆN PHÉP TÍNH
a) 2x(x^2-4y)
b)3x^2(x+3y)
c) -1/2x^2(x-3)
d) (x+6)(2x-7)+x
e) (x-5)(2x+3)+x
II phân tích đa thức thành nhân tử
a) 6x^2+3xy
b) 8x^2-10xy
c) 3x(x-1)-y(1-x)
d) x^2-2xy+y^2-64
e) 2x^2+3x-5
f) 16x-5x^2-3
g) x^2-5x-6
IIITÌM X BIẾT
a)2x+1=0
b) -3x-5=0
c) -6x+7=0
d)(x+6)(2x+1)=0
e)2x^2+7x+3=0
f) (2x-3)(2x+1)=0
g) 2x(x-5)-x(3+2x)=26
h) 5x(x-1)=x-1
IV TÌM GTNN,GTLN.
a) tìm giá trị nhỏ nhất
x^2-6x+10
2x^2-6x
b) tìm giá trị lớn nhất
4x-x^2-5
4x-x^2+3
bn ko bik lm hay sao, hay là bn chỉ đăng đề lên thôi
sao nhìu... z p , đăq từq câu 1 thôy nha p
I) THỰC HIỆN PHÉP TÍNH
a) 2x(x^2-4y)
b)3x^2(x+3y)
c) -1/2x^2(x-3)
d) (x+6)(2x-7)+x
e) (x-5)(2x+3)+x
II phân tích đa thức thành nhân tử
a) 6x^2+3xy
b) 8x^2-10xy
c) 3x(x-1)-y(1-x)
d) x^2-2xy+y^2-64
e) 2x^2+3x-5
f) 16x-5x^2-3
g) x^2-5x-6
IIITÌM X BIẾT
a)2x+1=0
b) -3x-5=0
c) -6x+7=0
d)(x+6)(2x+1)=0
e)2x^2+7x+3=0
f) (2x-3)(2x+1)=0
g) 2x(x-5)-x(3+2x)=26
h) 5x(x-1)=x-1
IV TÌM GTNN,GTLN.
a) tìm giá trị nhỏ nhất
x^2-6x+10
2x^2-6x
b) tìm giá trị lớn nhất
4x-x^2-5
4x-x^2+3
Ôi trời sao lắm thế ít thôi bạn nên tách ra mà bạn cần gấp lắm à
đúng rồi pn. giúp mik đc bài nào cũng đc
Tìm x biết: a) (2-x).x2< hoặc = 0. b)(x-7).(x+3)<0. c) (x+4).(x+3)>0. d) (x2+4x).(5-x)<0. e) x/x+1>0. f) 2x-1/2-x< hoặc = 0. Bài 2: tìm giá trị nhỏ nhất của các biểu thức sau: a) A=x2+y2+2014. b) B=(x+30)2+(y-4)2+17 c)C=(y-9)2 + |x-3| -1. d) D=x4 +11. e) E=-2014/|x|+2015. f)F=|x|+214/215
a) Ta có: \(x^2\ge0\forall x\in Q\)
\(y^2\ge0\forall x\in Q\)
\(\Rightarrow x^2+y^2+2014\ge2014\forall x\in Q\)
Dấu giá trị nhỏ nhất của biểu thức là 2014, xảy ra khi \(\left\{{}\begin{matrix}x^2=0\\y^2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=0\end{matrix}\right.\)
b, Ta có: \(\left(x+30\right)^2\ge0\forall x\in Q\)
\(\left(y-4\right)^2\ge0\forall x\in Q\)
\(\Rightarrow\left(x+30\right)^2+\left(y-4\right)^2+17\ge17\forall x\in Q\)
Dấu giá trị nhỏ nhất của biểu thức là 17, xảy ra khi \(\left\{{}\begin{matrix}\left(x+30\right)^2=0\\\left(y-4\right)^2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-30\\y=4\end{matrix}\right.\)
c, Ta có: \(\left(y-9\right)^2\ge0\forall x\in Q\)
\(\left|x-3\right|\ge0\forall x\in Q\)
\(\Rightarrow\left(y-9\right)^2+\left|x-3\right|^2-1\ge-1\forall x\in Q\)
Dấu giá trị nhỏ nhất của biểu thức là -1 xảy ra khi \(\left\{{}\begin{matrix}\left(y-9\right)^2=0\\\left|x-3\right|=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=9\\x=3\end{matrix}\right.\)
a) \(\left(2-x\right)x^2\le0\)
Ta có: \(\left(2-x\right)x^2=0\Leftrightarrow\left[{}\begin{matrix}x^2=0\\2-x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
Vì \(x^2\ge0\Rightarrow\left(2-x\right)x^2\Leftrightarrow2-x< 0\Leftrightarrow2< x\)
Vậy ......
b, \(\left(x-7\right)\left(x+3\right)< 0\Leftrightarrow\left[{}\begin{matrix}x-7< 0\\x+3< 0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x< 7\\x< -3\end{matrix}\right.\)
Vây........
c, \(\left(x+4\right)\left(x+3\right)\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x+4>0\\x+3>0\end{matrix}\right.\\\left\{{}\begin{matrix}x+4< 0\\x+3< 0\end{matrix}\right.\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x>-4\\x>-3\end{matrix}\right.\\\left\{{}\begin{matrix}x< -4\\x< -3\end{matrix}\right.\end{matrix}\right.\)
Vậy..............
Bài 1: Phân tích đa thức thành nhân tử
a. 5x - 20 y
b. 5.(x-1) - 3x.(x-1)
c. x.(x+1) -5x - 5y
d. ( x+y)^2-(x-y)^2
e. (3x+1)^2- (x+1)^2
Bài 2 . Tìm x biết
a. x + 5x^2=0
b. x+1=( x+1)^2
c. x^3 + x= 0
d. x^3 -0.25x = 0
e. x^2 - 10x = -25
Lần sau ghi tách ra tí bạn ơi ;v
--------------------------------
1. a) \(5x-20y=5\left(x-4y\right)\)
b) \(5\left(x-1\right)-3x\left(x-1\right)=\left(x-1\right)\left(5-3x\right)\)
c) \(x\left(x+1\right)-5x-5=x\left(x+1\right)-5\left(x+1\right)\)
\(=\left(x+1\right)\left(x-5\right)\)
d) \(\left(x+y\right)^2-\left(x-y\right)^2\)
\(=\left(x+y+x-y\right)\left(x+y-x+y\right)\)
\(=4xy\)
e) \(\left(3x+1\right)^2-\left(x+1\right)^2\)
\(=\left(3x+1+x+1\right)\left(3x+1-x-1\right)\)
\(=2x\left(4x+2\right)\)
2. a) \(x+5x^2=0\)
\(\Leftrightarrow x\left(1+5x\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\1+5x=0\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{-1}{5}\end{matrix}\right.\)
Vậy...
b) \(x+1=\left(x+1\right)^2\)
\(\Leftrightarrow x+1-x^2-2x-1=0\)
\(\Leftrightarrow-x^2-x=0\)
\(\Leftrightarrow-x\left(x+1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}-x=0\\x+1=0\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}x=0\\x=-1\end{matrix}\right.\)
Vậy...
c) \(x^3+x=0\)
\(\Leftrightarrow x\left(x^2+1\right)=0\)
Vì \(x^2+1>0\Rightarrow x=0\)
Vậy...
d) \(x^3-0,25x=0\)
\(\Leftrightarrow x\left(x^2-0,25\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x^2-0,25=0\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}x=0\\x=\pm0,5\end{matrix}\right.\)
Vậy..
e) \(x^2-10x=-25\)
\(\Leftrightarrow x^2-10x+25=0\)
\(\Leftrightarrow\left(x-5\right)^2=0\)
\(\Rightarrow x-5=0\)
\(\Rightarrow x=5\)
Vậy...
Bài 3: tìm x biết:
A) 16x^ ^ 2-(4x-5)^ ^ 2=0
B) (x+1)^ ^ 2-2(x^ ^ 2-1)+ (x-1)^ ^ 2=0
C) x^ ^ 3-8=0
D) 27x^ ^ 3+1/27=0
E) (3x+5)^ ^ 2-16=0
1/ tính
a,1+3+5+7+...+9
b,1+3+5+7+...+99
c,2+4+6+8+...+10
d,36+37+38+...+70
2/tìm x
a,3x+15=30
b,72-x=64+2x
c,45x-3x=40+2x
d,3x+x=56
e,x-3=0
f,42x=172+x
g,3x=0
h,18.[x-1]=18
i,420.[x-2]=0
Gợi ý thôi nha:
1.
Bước 1: Tính số số hạng có trong dãy: (Số hạng lớn nhất của dãy - số hạng bé nhất của dãy): khoảng cách giữa hai số hạng liên tiếp trong dãy + 1
Bước 2: Tính tổng của dãy: (Số hạng lớn nhất của dãy + số hạng bé nhất của dãy) x số số hạng có trong dãy : 2
VD:
Ví dụ 1: Tính giá trị của A biết:
A = 1 + 2 + 3 + 4 + ........................... + 2014.
Phân tích: Đây là dạng bài cơ bản trong dạng bài tính tổng của dãy có quy luật cách đều, chúng ta hướng dẫn học sinh tính giá trị của A theo 2 bước cơ bản ở trên.
Bài giải
Dãy số trên có số số hạng là:
(2014 – 1) : 1 + 1 = 2014 (số hạng)
Giá trị của A là:
(2014 + 1) x 2014 : 2 = 2029105
Đáp số: 2029105
2.
a. 3x+15=30
3x=30–15
3x=15
x=15:3
x=5
e) x—3=0
x=0+3
x=3
g)3x=0
x=0:3
x=0
h)18.(x—1)=18
x-1=18:18
x—1=1
x=1+1
x=2
i) 420.(x—2)=0
x—2=0:420
x—2=0
x=0+2
x=2
các bạn làm đầy đủ giúp mình nha ,cảm ơn >_<
Bài 1
a,Số số hạng là:(9-)1:2+1=5
Tổng của dãy số là:(9+1)x5 :2=25
b,Số số hạng là:(99-1):2+1=50
Tổng của dãy số là:(99+1)x50:2=2500
c,Số số hạng là:(10-2):2+1=5
Tổng của dãy số là:(10+2)x5:2=30
d,Số số hạng của dãy là:(70-36):1+1=35
Tổng của dãy số là:(70+36)x35:2=1855
mik làm bài 1 thôi nha