Cho biểu thức f ( x ) = 1 2018 x + 2018 . Tính tổng
S = 2018 [ f ( - 2017 ) + f ( - 2016 ) + . . . + f ( 0 ) + f ( 1 ) + . . . + f ( 2018 ) ]
Những câu hỏi liên quan
Cho hàm số y f(x) có
f
(
x
)
1
x
+
1
. Biết rằng f(0) 2018. Giá trị của biểu thức f(3)-f(1) bằng: A. ln2 B. ln4 C. ln3 D. 2ln2
Đọc tiếp
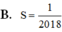
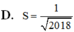
Cho hàm số y = f(x) có f ' ( x ) = 1 x + 1 . Biết rằng f(0)= 2018. Giá trị của biểu thức f(3)-f(1) bằng:
A. ln2
B. ln4
C. ln3
D. 2ln2
Cho hàm số
y
f
(
x
)
2019
l
n
e
x
2019
+
e
. Tính giá trị biểu thức
A
f
’
(
1
)
+...
Đọc tiếp
Cho hàm số y = f ( x ) = 2019 l n e x 2019 + e . Tính giá trị biểu thức A = f ’ ( 1 ) + f ’ ( 2 ) + … + f ’ ( 2018 )
A. 2018
B. 1009
C. 2017 2
D. 2019 2
1. Cho biểu thức B :
\(B=x^{2017}-2018.x^{2016}+2018.x^{2015}-2018.x^{2014}+...-2018.x^2+2018.x-1\)
TÍNH GIÁ TRỊ BIỂU THỨC VỚI x=2017
Tìm giá trị nhỏ nhất của biểu thức:
a) f(x) = |x - 5| - 5
b) g(x) = |x + 1| + |x + 2018|
a) f(x) đạt gtnn bằng -5 tại x=5
b) g(x) đạt gtnn tại 2017 tại x=-1 hoặc x=-2018
Đúng 0
Bình luận (0)
a)tìm giá trị nhỏ nhất của biểu thức E = |x-30|+|y-4|+(z-2018)^2
b)tìm giá trị lớn nhất của biểu thức F = 19-|x-5|-(y-2018)^2
1. Cho biểu thức B :
\(B=x^{2017}-2018.x^{2016}+2018.x^{2015}-2018.x^{2014}+...-2018.x^2+2018.x-1\)
TÍNH GIÁ TRỊ BIỂU THỨC VỚI x=2017
3. Cho : \(\frac{xy+1}{9}=\frac{yz+2}{15}=\frac{xz+3}{27}\)và xy +yz + zx=11 . TÌM x,y,z
Cho hàm số \(y=f(x)=|x|+1\)
Biết \(y_1=f(1); y_2=f(1); y_3=f(2); ...; y_2019=f(2018)\)
Tính giá trị biểu thức \(A=y_1+y_2+...+y_2019\)
Ta có: y= f(x) = |x| + 1
f(1) = |1| + 1 = 1 + 1 = 2 => y1 = y2 = 2
f(2) = |2| + 1 = 2 + 1 = 3 => y3 = 3
f(3) = |3| + 1 = 3 + 1 = 4 => y4 = 4
...
f(2018) = |2018| + 1 = 2018 + 1 = 2019 => y2019 = 2019
Do đó: A = y1 + y2 + y3 + ... + y2019
= 2 + 2 + 3 + ... + 2019
= 2 + (2 + 3 + ... + 2019)
Tổng 2 + 3 + ... + 2019 có số số hạng là: 2019 - 2 + 1 = 2018
Suy ra: A = 2 + [(2 + 2019) . 2018 : 2]
= 2 + 2 039 189
= 2 039 191
Đúng 0
Bình luận (0)
Tìm giá trị nhỏ nhất của biểu thức
a,f(x)=|x-5|-5
b, g(x)=|x+1|+|x+2018|
a: \(f\left(x\right)=\left|x-5\right|-5>=-5\)
Dấu '=' xảy ra khi x=5
b: \(g\left(x\right)=\left|x+2018\right|+\left|-x-1\right|\)
\(\Leftrightarrow g\left(x\right)\ge x+2018-x-1=2017\)
Dấu '=' xảy ra khi x+2018>=0 và -x-1>=0
=>-2018<=x<=-1
Đúng 0
Bình luận (0)
Tìm giá trị nhỏ nhất của biểu thức:
a) f(x) = |x - 5| - 5
b) g(x) = |x + 1| + |x + 2018|
a: \(f\left(x\right)=\left|x-5\right|-5>=-5\)
Dấu '=' xảy ra khi x=5
b: \(g\left(x\right)=\left|x+2018\right|+\left|-x-1\right|\ge2017\forall x\)
Dấu '=' xảy ra khi x+2018>=0và -x-1>=0
=>-2018<=x<=-1
Đúng 0
Bình luận (0)