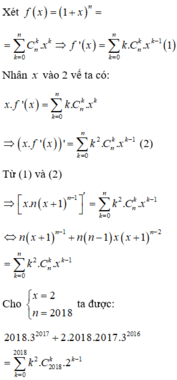tính tổng S=12+22+32+...+202-(1+2+3+...+20)

Những câu hỏi liên quan
Tính tổng : S=12+22+32+....+202 - (1+2+3....+20) ta thu được kết quả S=....
Số số hạng của 12 + 22 + 32 + .. + 202 : (202 - 1) : 10 + 1 = 20
Số số hạng của 1 + 2 + 3 + .. + 20 : (20 - 1) + 1 = 20
S = {(12+ 202) - (1 + 20)} x 20 : 2 = 1930
Lúc nãy nhầm làm tổng của 2 dãy
Đúng 0
Bình luận (0)
Số số hạng: (202 - 12) : 10 + 1 =20 và 1 + 2 + 3 + ...+ 20 cũng có 20 số hạng
\(\Rightarrow\)S = ( 12 + 202 + 1 + 20 ) x 20 : 2 = 2350
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
biết:12+22+32+...+102=385.Tính tổng S=22+42+62+...+202
Ta có \(2^2+4^2+...+20^2=2^2\left(1^2+2^2+...+10^2\right)=2^2.385=1540\).
Đúng 1
Bình luận (0)
Đố: Biết rằng 12 + 22 + 32 + ... + 102 = 385, đố em tính nhanh được tổng:
S = 22 + 42 + 62 + ... + 202
S = 22 + 42 + 62 + ... + 202
= (2.1)2 + (2.2)2 + (2.3)2 ... (2.10)2
= 22.12 + 22.22 + 22.32 + ... + 22.102
= 22 (12 + 22 + ... + 102 )
= 4 . 385 = 1540
Đúng 0
Bình luận (0)
Biết rằng 12 + 22 + 32 +…+ 102 = 385, đố em tính nhanh được tổng S = 22 + 42 + 62 + … + 202
GIÚP MÌNH NHA,MÌNH K CHO!!!
Ta có : \(1^2+2^2+3^2+.....+10^2=385\)
\(\Leftrightarrow2^2\left(1^2+2^2+3^2+.....+10^2\right)=2^2.385\)
\(\Leftrightarrow2^2+4^2+6^2+.....+20^2=4.385\)
\(\Leftrightarrow2^2+4^2+6^2+.....+20^2=1540\)
Đúng 0
Bình luận (0)
Sửa đề: CHo 12+22+...+102=385. Tính S = 22+42 +...+ 202
S = 22 + 42 +...+ 202
= (1.2)2 + (2.2)2 +...+ (2.10)2
= 12.22 + 22.22 +...+ 22.102
= 22(12 + 22 +...+ 102)
= 4.385
= 1540
Đúng 2
Bình luận (0)
S= 1^2 . 2^2 + 2^2 . 2^2 + ... + 10^2 . 2^2
= 4. ( 1^2 + 2^2 +...+ 10^2) = 4 . 385 = 1540
chúc bạn học giỏi
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Cho biết:
1
2
+
2
2
+
3
2
+
.
.
.
+
10
2
385
Tính nhanh giá trị của biểu thức sau
S
12
2
+
14...
Đọc tiếp
Cho biết: 1 2 + 2 2 + 3 2 + . . . + 10 2 = 385
Tính nhanh giá trị của biểu thức sau S = 12 2 + 14 2 + 16 2 + 18 2 + 20 2 - 1 2 + 3 2 + 5 2 + 7 2 + 9 2
A. 1155
B. 5511
C. 5151
D. 1515
Tính các tổng sau:
1, S=1-2+3_4+..+25-26
2, S=1-3+5-7+...+49-51
3, S=-1+3-5+7-...-53+55
4, S=2-4+6-8+...+22-24
5, S=-2+4-6+8-...-26+28
6, S=2-5+8-11+...-29+32
7, S=-1+5-9-13-...-41-45
8, S=1-5+9-13+...++89-93
9, S=2-4+6-8+...+202-204
10, S=1-6=11-16+21-26+...+171-176
huhu giúp mình với ạ 2h chiều nay mình phải nộp r =(((
Tính các tổng sau:
1, S=1-2+3_4+..+25-26
S =-1+3-5+7-...-53+55 ( có 28 số hạng )
= (-1+3)+(-5+7)+...+(-53+55) ( có 28:2=14 nhóm )
= 2+2+...+2
= 2 . 14
= 28
Đúng 1
Bình luận (0)
3
S =-1+3-5+7-...-53+55 ( có 28 số hạng )
= (-1+3)+(-5+7)+...+(-53+55) ( có 28:2=14 nhóm )
= 2+2+...+2
= 2 . 14
= 28
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Tổng
S
1
2
.
C
2018
1
.2
0
+
2
2
.
C
2018
2
.2
1
+
3
2
.
C
2018
3
.2
2...
Đọc tiếp
Tổng S = 1 2 . C 2018 1 .2 0 + 2 2 . C 2018 2 .2 1 + 3 2 . C 2018 3 .2 2 + ... + 2018 2 . C 2018 2018 .2 2017 = 2018.3 a . 2. b + 1 với a,b là các số nguyên dương và 2. b + 1 không chia hết cho 3. Tính a + b .
A. 2017
B. 4035
C. 4043
D. 2018
bài 1:cho S = 1+2+22+23+...+22023
a. tính tổng
b.cho B = 22024 so sánh S và B
bài 2: tính tổng H=3+32+33+...+32022
Bài 1
a) S = 1 + 2 + 2² + 2³ + ... + 2²⁰²³
2S = 2 + 2² + 2³ + 2⁴ + ... + 2²⁰²⁴
S = 2S - S = (2 + 2² + 2³ + ... + 2²⁰²⁴) - (1 + 2 + 2² + 2³)
= 2²⁰²⁴ - 1
b) B = 2²⁰²⁴
B - 1 = 2²⁰²⁴ - 1 = S
B = S + 1
Vậy B > S
Đúng 2
Bình luận (0)
a,
\(S=1+2+2^2+...+2^{2023}\)
\(2S=2+2^2+2^3+...+2^{2024}\)
\(\Rightarrow S=2^{2024}-1\)
b.
Do \(2^{2024}-1< 2^{2024}\)
\(\Rightarrow S< B\)
2.
\(H=3+3^2+...+3^{2022}\)
\(\Rightarrow3H=3^2+3^3+...+3^{2023}\)
\(\Rightarrow3H-H=3^{2023}-3\)
\(\Rightarrow2H=3^{2023}-3\)
\(\Rightarrow H=\dfrac{3^{2023}-3}{2}\)
Đúng 3
Bình luận (0)
Bài 2
H = 3 + 3² + 3³ + ... + 3²⁰²²
⇒ 3H = 3² + 3³ + 3⁴ + ... + 3²⁰²³
⇒2H = 3H - H
= (3² + 3³ + 3⁴ + ... + 3²⁰²³) - (3 + 3² + 3³ + ... + 3²⁰²²)
= 3²⁰²³ - 3
⇒ H = (3²⁰²³ - 3) : 2
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
M = 1002– 992 + 982 – 972 + … + 22 – 12;
N = (202+ 182 + 162 + … + 42 + 22) – (192 + 172 + 152 + … + 32 + 12);
P = (-1)n.(-1)2n+1.(-1)n+1.
a:
Số số hạng trong dãy M là:
(1002-12):10+1=100(số)
=>Sẽ có 50 cặp (1002;992); (982;972);....;(22;12) có hiệu bằng 10
\(M=1002-992+982-972+...+22-12\)
\(=\left(1002-992\right)+\left(982-972\right)+...+\left(22-12\right)\)
\(=10+10+...+10\)
=10*50=500
b: \(N=\left(202+182+...+42+22\right)-\left(192+172+...+32+12\right)\)
\(=\left(202-192\right)+\left(182-172\right)+...+\left(22-12\right)\)
=10+10+...+10
=10*10=100
Đúng 0
Bình luận (0)
Tổng
S
1
2
.
C
2018
1
.
2
0
+
2
2
.
C
2018
2
.
2
1
+
3
2
.
C
2018
3
.
2...
Đọc tiếp
Tổng S = 1 2 . C 2018 1 . 2 0 + 2 2 . C 2018 2 . 2 1 + 3 2 . C 2018 3 . 2 2 + . . . + 2018 2 . C 2018 2018 . 2 2017 = 2018 . 3 a . ( 2 b + 1 ) ,
với a, b là các số nguyên dương và (2b+1) không chia hết cho 3.
Tính a+b.
A. 2017
B. 4035
C. 4034
D. 2018