ĐÁP ÁN: A

Chọn A.

Theo giải thiết

Tập hợp điểm M là đường tròn đường kính BC.

Vì E ;  F là hai điểm cố định nên từ đẳng thức (*) suy ra tập hợp các điểm M là trung trực của đoạn thẳng EF.

Gọi I là trung điểm của AB suy ra I cũng là trung điểm của EF.

Vậy tập hợp các điểm M thỏa mãn 2 M A → + M B → = M A → + 2 M B →  là đường trung trực của đoạn thẳng AB.

Chọn A.

Chọn điểm E thuộc đoạn AB sao cho EB = 2EA   ⇒ 2 E A → + E B → = 0 → .

Chọn điểm F thuộc đoạn AB sao cho FA = 2FB  ⇒ 2 F B → + F A → = 0 → .

Ta có 

2 M A → + M B → = M A → + 2 M B → ⇔ 2 M E → + 2 E A → + M E → + E B → = M F → + F A → + 2 M F → + 2 F B → ​

⇔ 3   M E → + 2   E A → + E B → ⏟ 0 → = 3   M F → +   F A → + 2 F B → ⏟ 0 → ⇔ 3   M E → = 3   M F → ⇔ M E = M F . ( * )

Vì E ; F là hai điểm cố định nên từ đẳng thức (*) suy ra tập hợp các điểm M là trung trực của đoạn thẳng EF.

Gọi I là trung điểm của AB suy ra I cũng là trung điểm của EF

Vậy tập hợp các điểm M thỏa mãn  2 M A → + M B → = M A → + 2 M B → là đường trung trực của đoạn thẳng AB.

Chọn A.

a,gọi I là trung điểm của AB, vì A và B là 2 điểm cố định => I cũng cố định
=> vt IA+vt IB=0
=>|vt MA+vtMB|=|vtMA-vtMB|
<=> |vtMI+vtIA+vtMI+vtIB|=|vtMI+vtMA-vtMI-vtIB|
<=>|2.vtMI|=|vtBA|
<=> 2,MI=BA
=> MI=BA/2
=> M thuộc (I;AB/2)

Mình cảm ơn bạn nhiều ạ ^^ 

ko cần cảm ơn đâu vì mik tháy bạn cần gấp nên mik đưa cho câu trả lời ý mà

Chọn B.

Theo giả thiết

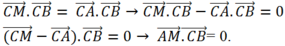
Tập hợp điểm M là đường thẳng đi qua A và vuông góc với BC.

\(\Leftrightarrow\overrightarrow{CB}\left(\overrightarrow{CA}-\overrightarrow{CM}\right)=0\)

\(\Leftrightarrow\overrightarrow{CB}.\left(\overrightarrow{CA}+\overrightarrow{MC}\right)=0\)

\(\Leftrightarrow\overrightarrow{CB}.\overrightarrow{MA}=0\)

Tập hợp M là đường thẳng qua A và vuông góc BC