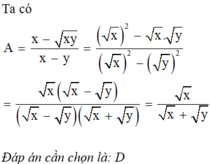Rút gọn biểu thức: x(x – y) + y(x – y)

Những câu hỏi liên quan
Rút gọn biểu thức x(x+y)-y(x+y)+x^2 + y^2
Lời giải:
$x(x+y)-y(x+y)+x^2+y^2=(x-y)(x+y)+x^2+y^2$
$=x^2-y^2+x^2+y^2=2x^2$
Đúng 0
Bình luận (0)
rút gọn biểu thức x(x-y)+y(x-y)
Rút gọn biểu thức x(x-y)-y(y-x) ta được
\(x\left(x-y\right)-y\left(y-x\right)=\left(x+y\right)\left(x-y\right)=x^2-y^2\)
Đúng 1
Bình luận (0)
x(x-y)-y(y-x) = x2-xy-(y2-xy) = x2-xy-y2+xy = x2-y2
Đúng 1
Bình luận (0)
x(x-y)-y(y-x) = x2-xy-(y2-xy) = x2-xy-y2+xy = x2-y2
Tham thảo
Đúng 1
Bình luận (0)
rút gọn biểu thức ( chỉ mình cách rút gọn lun nhea , mơn nhìu ạ )
x(x-y)+y(x-y)
\(x\left(x-y\right)+y\left(x-y\right)\)
\(=x^2-xy+xy-y^2\)
\(=x^2-y^2\)
Đúng 0
Bình luận (0)
Rút gọn biểu thức sau: (x + y + z)2 – 2(x + y + z)(x + y) + (x + y)2
(x + y + z)2 – 2.(x + y + z).(x + y) + (x + y)2
= [(x + y + z) – (x + y)]2 (Áp dụng HĐT (2) với A = x + y + z ; B = x + y)
= z2.
Đúng 0
Bình luận (0)
Rút gọn biểu thức: 2(x – y)(x + y) + x + y 2 + x - y 2
2(x – y)(x + y) + x + y 2 + x - y 2
= x + y 2 +2( x+ y).(x- y) + x - y 2
(áp dụng hằng đẳng thức thứ 1với A = x+ y, B = x- y)
= x + y + x - y 2 = 2 x 2 = 4 x 2
Đúng 0
Bình luận (0)
Rút gọn biểu thức: A=(x-y)^2+(x+y)^2-2(x+y)(x-y)-4(y^2-1)
\(A=\left(x-y\right)^2+\left(x+y\right)^2-2\left(x+y\right)\left(x-y\right)-4\left(y^2-1\right)\)
\(=\left(x-y-x-y\right)^2-4\left(y^2-1\right)\)
\(=\left(-2y\right)^2-4y^2+4=4\)
Đúng 1
Bình luận (0)
Với x, y
≥
0;
x
≢
y
, rút gọn biểu thức
x
-
xy
x
-
y
ta được? A.
x
x
-
y
B.
1
x...
Đọc tiếp
Với x, y ≥ 0; x ≢ y , rút gọn biểu thức x - xy x - y ta được?
A. x x - y
B. 1 x - y
C. y x - y
D. x x + y
rút gọn biểu thức
\(\dfrac{x\sqrt{y}-y\sqrt{x}}{x-\sqrt{xy}+y}\)