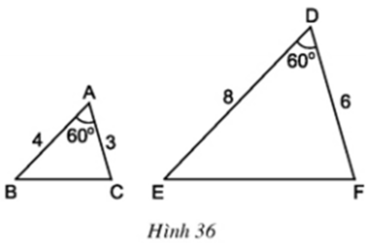
Cho hai tam giác ABC và DEF có kích thước như trong hình 36.
- So sánh các tỉ số A B D E v à A C D F .
- Đo các đoạn thẳng BC, EF. Tính tỉ số B C E F , so sánh với các tỉ số trên và dự đoán sự đồng dạng của hai tam giác ABC và DEF.
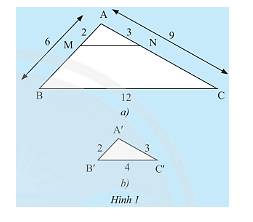
Cho tam giác \(ABC\) và tam giác \(A'B'C'\) có các kích thước như Hình 1. Trên cạnh \(AB\) và \(AC\) của tam giác \(ABC\) lần lượt lấy hai điểm \(M,N\) sao cho \(Am = 2cm,AN = 3cm\).
a) So sánh các tỉ số \(\frac{{A'B'}}{{AB}},\frac{{A'C'}}{{AC}},\frac{{B'C'}}{{BC}}\).
b) Tính độ dài đoạn thẳng \(MN\).
c) Em có nhận xét gì về mối liên hệ giữ các tam giác \(ABC,AMN\) và \(A'B'C'\)?
a) Ta có: \(\frac{{A'B'}}{{AB}} = \frac{2}{6} = \frac{1}{3},\frac{{A'C'}}{{AC}} = \frac{3}{9} = \frac{1}{3},\frac{{B'C'}}{{BC}} = \frac{4}{{12}} = \frac{1}{3}\). Do đó, các tỉ số trên bằng nhau.
b) Ta có: \(\frac{{AM}}{{AB}} = \frac{2}{6} = \frac{1}{3};\frac{{AN}}{{AC}} = \frac{3}{9} = \frac{1}{3}\)
Vì \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} \Rightarrow MN//BC\) (định lí Thales đảo)
Vì \(MN//BC \Rightarrow \frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}}\) (Hệ quả của định lí Thales)
Do đó, \(\frac{{MN}}{{BC}} = \frac{1}{3} \Leftrightarrow \frac{{MN}}{{12}} = \frac{1}{3} \Rightarrow MN = \frac{{12.1}}{3} = 4\).
Vậy \(MN = 4cm\).
c) Vì \(MN//BC \Rightarrow \Delta ABC\backsim\Delta AMN\) (định lí)(1)
Xét tam giác \(AMN\) và tam giác \(A'B'C'\) ta có:
\(AM = A'B' = 2cm;AN = A'C' = 2cm;MN = B'C' = 4cm\)
Do đó, \(\Delta AMN = \Delta A'B'C'\) (c.c.c)
Vì \(\Delta AMN = \Delta A'B'C'\) nên \(\Delta AMN\backsim\Delta A'B'C'\) (2)
Từ (1) và (2) suy ra, \(\Delta ABC\backsim\Delta A'B'C'\).
Cho hai tam giác ABC và A'B'C' có kích thước như trong hình 35.
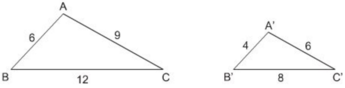
Hình 35
a) ΔABC và ΔA'B'C' có đồng dạng với nhau không? Vì sao?
b) Tính tỉ số chu vi của hai tam giác đó.
a) Ta có:
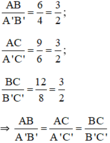
⇒ ΔABC 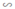 ΔA’B’C’ (c.c.c).
ΔA’B’C’ (c.c.c).
b) Ta có:
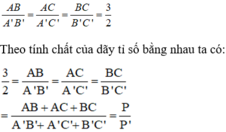
Vậy tỉ số chu vi của tam giác ABC và chu vi của tam giác A’B’C’ là 3/2.
Cho tam giác ABC có góc A=68 độ ; góc B=60 độ và 3 đường cao AD;BE;CF. Biết diện tích tam giác ABC=14,99283 cm vuông
a) Tính diện tích hình chữ nhật có hai kích thước là AB và AC
b) Tính diện tích tam giác DEF
 Cho hình thang ABCD có các kích thước như hình vẽ bên.
Cho hình thang ABCD có các kích thước như hình vẽ bên.
A) tính diện tích hình thang ABCD
B) tính diện tích hình tam giác ABD và hình BDC
C) tính tỉ số phần trăm của diện tích hình tam giác ABD và BDC.
a) Diện tích hình thang ABCD là
`(15+12)*9 :2 = 121,5(cm^2)`
b) Diện tích tam giác BCD là
`9*15 :2 = 67,5(cm^2)`
Diện tích tam giác ABD
`9*12 :2 = 54(cm^2)`
Tỉ số `%` của tam giác ABD và tam giác BDC
`54/(67,5) *100% = 80%`
Cho hình tam giác ABC. Trên cạnh BC lấy điểm D sao cho BD = 1/3 BC. Nối A với D. Trên AD lấy điểm E sao cho AE = 2/3 AD. Nối E với B và E với C.
a) Hãy so sánh diện tích hai tam giác ABE và EDC
b) Tìm tỉ số diện tích hai tam giác EBD và AEC
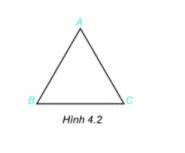
Cho tam giác đều ABC như hình 4.2.
1. Gọi tên các đỉnh, cạnh góc của tam giác đều ABC.
2. Dùng thước thẳng để đo và so sánh các cạnh của tam giác ABC.
3. Sử dụng thước đo góc để đo và so sánh các góc của tam giác ABC.
1) Các đỉnh : A, B, C
Các cạnh: AB, BC, AC
Các góc: \(\widehat A,\,\widehat B,\,\widehat C\)
2) AB =3 cm, AC = 3 cm, BC = 3 cm nên các cạnh của tam giác ABC bằng nhau
3) \(\widehat A = 60^0; \widehat B =60^0; \widehat C=60^0\) nên các góc của tam giác ABC bằng nhau và bằng 60o
Cho hai tam giác ABC và A'B'C' có kích thước như trong hình 35
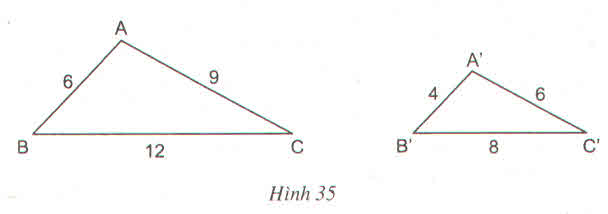
a) \(\Delta ABC\) và \(\Delta A'B'C'\) có đồng dạng với nhau không ? Vì sao ?
b) Tính tỉ số chu vi của hai tam giác đó ?
= = = 3/2
=> ∆ABC ∽ ∆A'B'C'
b) = 3/2
a)Xét \(\Delta ABC\) và \(\Delta A'B'C'\) có:
\(\dfrac{AB}{A'B'}=\dfrac{BC}{B'C'}=\dfrac{AC}{A'C'}\)
\(\Rightarrow\Delta ABC\)∽\(\Delta A'B'C'\)(c.c.c)
b)Từ câu a và áp dụng tính chất tỉ lệ thức ta có:
\(\dfrac{AB}{A'B'}=\dfrac{BC}{B'C'}=\dfrac{AC}{A'C'}=\dfrac{AB+BC+AC}{A'B'+B'C'+A'C'}=\dfrac{3}{2}\)
mà \(C_{ABC}=AB+BC+AC\)
\(C_{A'B'C'}=A'B'+B'C'+A'C'\)
Vậy tỉ số chu vi của \(\Delta ABC\) và \(\Delta A'B'C'\)là:
\(\dfrac{C_{ABC}}{C_{A'B'C'}}=\dfrac{3}{2}\)
a)\(\Delta\)ABC và \(\Delta\)A'B'C' có đồng dạng với nhau
vì:AB/A'B' = BC/B'C' = CA/C'A' = 3/2
b)AB/A'B' = BC/B'C' = CA/C'A' = 3/2
⇔AB+BC+CA/A'B' + B'C' + C'A'
⇔6+12+9/4+8+6 = 3/2
Cho tam giác DEF có: \(12\widehat{D}=10\widehat{E}=15\widehat{F}\)
a, So sánh các cạnh của tam giác DEF
b, Phân giác của góc E cắt DF tại M. So sánh DM và FM
a/ Ta có \(12\widehat{D}=15\widehat{F}\)
=> \(4\widehat{D}=5\widehat{F}\)
=> \(\widehat{D}=\frac{5}{4}\widehat{F}\)
=> \(\widehat{D}>\widehat{F}\)(1)
và \(10\widehat{E}=15\widehat{F}\)
=> \(2\widehat{E}=3\widehat{F}\)
=> \(\widehat{E}=\frac{3}{2}\widehat{F}\)
=> \(\widehat{E}>\widehat{F}\)(2)
Từ (1) và (2) => \(\widehat{D}>\widehat{E}>\widehat{F}\)
=> EF > DF > DE (quan hệ giữa góc và cạnh đối diện trong tam giác)
Cho tam giác ABC vuông tại A, có AB = 6cm, AC = 8cm , BC = 10cm và tam giác DEF vuông tại D có DE = 9cm, DF = 12cm, EF = 15cm.
a) Hai tam giác ABC và DEF có đồng dạng không? Vì sao?
b) Tính tỉ số chu vi của hai tam giác ấy?
a: Xét ΔABC vuông tại A và ΔDEF vuông tại D có
AB/DE=AC/DF
Do đó: ΔABC\(\sim\)ΔDEF
b: \(\dfrac{C_{ABC}}{C_{DEF}}=\dfrac{AB}{DE}=\dfrac{2}{3}\)