Trên đường tròn lượng giác hãy biểu diễn các cung có số đo

Khi biểu diễn trên đường tròn lượng giác các cung lượng giác nào trong các cung lượng giác có số đo dưới đây có cùng ngọn cung với cung lượng giác có số đo 42000
A.1300
B.1200
C.-1200
D.600
Chọn C.
Ta có 42000 = - 1200 + 12. 3600
nên cung có số đo – 1200 có ngọn cung trùng với ngọn cung có số đo 42000.
Số điểm biểu diễn cung lượng giác có số đo là nghiệm của phương trình cot x = tan x + 2 cos 4 x sin 2 x trên đường tròn lượng giác là
A. 2
B. 3
C. 6
D. 4
Đáp án D
ĐK: sin 2 x ≠ 0 .
Khi đó:
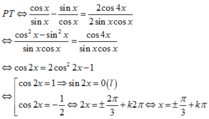
Do đó có 4 điểm x = ± π 3 ; x = 2 π 3 ; x = 4 π 3 biểu diễn nghiệm của PT đã cho.
Khi biểu diễn các cung lượng giác có số đo khác nhau trên đường tròn lượng giác, có thể xảy ra trường hợp các điểm cuối của chúng trùng nhau không ? Khi nào trường hợp này xảy ra?
Khi số đo hai cung lệch nhau k.2π (k ∈ Z) thì điểm cuối của chúng có thể trùng nhau.
Chẳng hạn các cung α = π/3 và β = π/3 + 2π , γ = π/3 - 2π có điểm cuối trùng nhau khi biểu diễn trên đường tròn lượng giác.
Số điểm biểu diễn cung lượng giác có số đo là nghiệm của phương trình c o t x = tan x + 2 . cos 4 x sin 2 x trên đường tròn lượng giác là
A. 2
B. 3
C. 6
D. 4
Khi biểu diễn các cung lượng giác có số đo khác nhau trên đường tròn lượng giác, có thể xảy ra trường hợp các điểm cuối của chúng trùng nhau không ? Khi nào trường hợp này xảy ra ?
Trường hợp này xảy ra khi chúng sai khác nhau bội của 3600 (hay bội của 2π)
Biểu diễn trên đường tròn lượng giác góc (cung) có số đo α:
a) α = 10350
b) α = 195π/3
c) α = π/2 + kπ, k∈Z
d) α = kπ
Cung có số đo \(\dfrac{\pi}{6}+\dfrac{k2\pi}{3}\left(k\in Z\right)\) biểu diễn được bao nhiêu điểm trên đường tròn lượng giác
Trên đường tròn lượng giác, hãy biểu diễn các góc lượng giác có số đo có dạng:
a) \(\frac{\pi }{4} + k\pi \,\,\left( {k \in Z} \right)\)
b) \(k\frac{\pi }{4}\,\,\left( {k \in Z} \right)\)
Trên đường tròn lượng giác, xác định điểm M biểu diễn các góc lượng giác có số đo sau: 2pi/3