Chọn C.
Ta có 42000 = - 1200 + 12. 3600
nên cung có số đo – 1200 có ngọn cung trùng với ngọn cung có số đo 42000.
Chọn C.
Ta có 42000 = - 1200 + 12. 3600
nên cung có số đo – 1200 có ngọn cung trùng với ngọn cung có số đo 42000.
Trên đường tròn lượng giác hãy biểu diễn các cung có số đo

Khi biểu diễn các cung lượng giác có số đo khác nhau trên đường tròn lượng giác, có thể xảy ra trường hợp các điểm cuối của chúng trùng nhau không ? Khi nào trường hợp này xảy ra?
Trên đường tròn lượng giác gốc A. Cho các cung lượng giác có điểm đầu A và có số đo như sau:
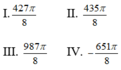
Các cung có điểm cuối trùng nhau là?
A. II và IV
B. I và II
C. I và III
D. I và IV
Trên đường tròn lượng giác gốc A cho các cung có số đo:

Hỏi các cung nào có điểm cuối trùng nhau?
A. Chỉ (I) và (II).
B. Chỉ (I), (II) và (III).
C. Chỉ (II), (III) và (IV).
D. Chỉ (I), (II) và (IV).
Chọn điểm A(1 ; 0) là điểm đầu của cung lượng giác trên đường tròn lượng giác. Tìm điểm cuối M của cung lượng giác có số đo 25π/4.
A. M là điểm chính giữa của cung phần tư thứ I.
B. M là điểm chính giữa của cung phần tư thứ II.
C. M là điểm chính giữa của cung phần tư thứ III.
D. M là điểm chính giữa của cung phần tư thứ IV.
Cho cung lượng giác AB có số đo là 15 rad. Tìm số lớn nhất trong các số đo của cung lượng giác điểm đầu A, điểm cuối B, có số đo âm.
Biểu diễn trên đường tròn lượng giác góc (cung) có số đo α:
a) α = 10350
b) α = 195π/3
c) α = π/2 + kπ, k∈Z
d) α = kπ
Trên đường tròn lượng giác cho điểm M xác định bởi số đo AM = 80 o trong đó A(1; 0). Gọi M' là điểm đối xứng với M qua đường phân giác của góc phần tư thứ II. Số đo của cung lượng giác AM' là:
A. 170 o B. - 200 o
C. 190 o D. 280 o
Trên đường tròn lượng giác bán kính 15cm, độ dài cung có số đo 3,4 rad là:
A. 51cm
B. 102cm
C. 160,14cm
D. 160,22cm