Cho hình 16. Hãy chứng minh rằng:
BE < BC;
Những câu hỏi liên quan
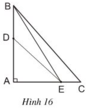
Cho hình 16. Hãy chứng minh rằng:
DE < BC.
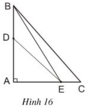
Trong hình vẽ D nằm giữa A và B ⇒ AD < AB
Ta có: ED, EB là hai đường xiên vẽ từ E đến đường AB
EA ⏊ AB tại A nên A là hình chiếu của E trên AB.
⇒ AD, AB lần lượt là hình chiếu của ED, EB trên AB
Trong hình vẽ D nằm giữa A và B ⇒ AD < AB nên ED < EB hay DE < BE (đường xiên nào có hình chiếu lớn hơn thì lớn hơn).
Kết hợp với kết quả câu a suy ra DE < BE < BC ⇒ DE < BC.
Đúng 0
Bình luận (0)
Cho hình 16 : Hãy chứng minh rằng :
a) BE < BC
b) DE < BC
a) Trong hình vẽ BE < BC là hai đường xiên vẽ từ B đến đường AC và AE, AC là hai hình chiếu của chúng vì AE < AC nên BE < BC
b) EB và ED là hai đường xiên vẽ từ E đến AB
AB và AD là hai hình chiếu của chúng
Vì AD < AB nên DE < BE
Ta có: BE < BC và DE < BE nên DE < BC
Đúng 0
Bình luận (0)
Hình thang ABCD có đáy AB, CD.
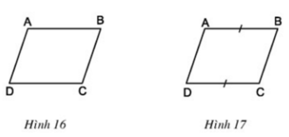
a) Cho biết AD // BC (h.16). Chứng minh rằng AD = BC, AB = CD.
b) Cho biết AB = CD (h.17). Chứng minh rằng AD // BC, AD = BC.
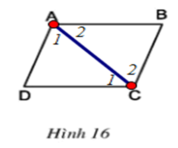
Hình thang ABCD có đáy AB, CD ⇒ AB // CD ⇒ ∠A2 = ∠C1 ̂ (hai góc so le trong)
Lại có: AD // BC ⇒ ∠A1 = ∠C2 (hai góc so le trong)
Xét ΔABC và ΔCDA có:
∠A2 = ∠C1 (cmt)
AC chung
∠A1 = ∠C2 (cmt)
⇒ ΔABC = ΔCDA (g.c.g)
⇒ AD = BC, AB = CD (các cặp cạnh tương ứng)
b)
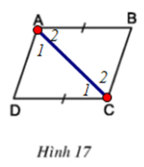
Xét ΔABC và ΔCDA có:
AC chung
∠A2 = ∠C1 (cmt)
AB = CD
⇒ ΔABC = ΔCDA (c.g.c)
⇒ AD = BC (hai cạnh tương ứng)
∠A1 = ∠C2 (hai góc tương ứng) ⇒ AD // BC (hai góc so le trong bằng nhau)
Đúng 2
Bình luận (0)
Cho tam giác ABC có các đường trung tuyến AD, BE và CF cắt nhau tại trọngtâm G (D ∈ BC, E ∈ AC, F ∈ AB). Trên tia đối của tia F C lấy điểm N sao cho F N F C.a) Chứng minh rằng ∆AF N ∆BF C. Từ đó, hãy suy ra rằng AN BC.b) Lấy K ∈ NF sao cho FK F G. Chứng minh rằng ∆AFK ∆BF G. Từ đó, hãy suy ra rằngAD BE + CF.c) Giả sử AGB ≤ 900. Chứng minh rằng F A F B ≤ F G. Từ đó, hãy chứng tỏ rằng AC + BC 3AB.
Đọc tiếp
Cho tam giác ABC có các đường trung tuyến AD, BE và CF cắt nhau tại trọng
tâm G (D ∈ BC, E ∈ AC, F ∈ AB). Trên tia đối của tia F C lấy điểm N sao cho F N = F C.
a) Chứng minh rằng ∆AF N = ∆BF C. Từ đó, hãy suy ra rằng AN = BC.
b) Lấy K ∈ NF sao cho FK = F G. Chứng minh rằng ∆AFK = ∆BF G. Từ đó, hãy suy ra rằng
AD < BE + CF.
c) Giả sử AGB \≤ 900
. Chứng minh rằng F A = F B ≤ F G. Từ đó, hãy chứng tỏ rằng AC + BC >
3AB.
giúp mình vs, mình đang cần gấp ạ !!!
Làm giúp em câu b với ạ Câu 16: Cho tam giác ABC cân tại A, đường cao BM, đường cao CN cắt nhau tại H. a) Chứng minh rằng: AH vuông góc với BC b) AH cắt BC tại I; E là trung điểm CH. Chứng minh rằng BE > 3/4 BC
b: BE>BC+CE
=BC+1/2CH
=BC+1/2*1/2(HB+HC)
=BC+1/4(HB+HC)>BC+1/4BC
=>BE>5/4BC>3/BC
Đúng 0
Bình luận (0)
cho tam giác abc có ab=6cm ac=8cm bc=10cm
a) hãy chứng minh abc là tam giác vuông
b) trên cạnh bc lấy e sao cho be=ba kẻ ed vuông góc ac (d thuộc ac)
chứng minh rằng bd là tia phân giác của b
c) gọi f là giao điểm của ed và ba .chứng minh rằng tam giác dec = tam giác daf từ đó suy ra df> de
d) cmr:ad vuông góc với cf
a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
b: Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
BA=BE
Do đó:ΔABD=ΔEBD
Suy ra: góc ABD= góc EBD
hay BD là tia phân giác của góc ABC
c: Xét ΔADF vuông tại A và ΔEDC vuông tại E có
DA=DE
\(\widehat{ADF}=\widehat{EDC}\)
Do đó: ΔADF=ΔEDC
Suy ra: DF=DC
mà DC>DE
nên DF>DE
d: Đề sai rồi bạn
Đúng 3
Bình luận (1)
Bài 1: Cho ΔABC vuông tại A, phân giác BE của góc B (E ∈ AC). Từ E kẻ ED ⊥ BC (D thuộc BC). Đường thẳng BE cắt tia BA tại F a) Chứng minh rằng ΔEAB ΔEDB b) Chứng minh rằng EC EF ( Vẽ hình, viết giả thiết kết luận )Bài 2: Cho ΔABC có AB AC. Gọi M là trung điểm của BC a) Chứng minh ΔABM ΔACM b) Chứng minh AM ⊥ BC c) Chứng minh AM là phân giác của góc BAC ( Vẽ hình, viết giả thiết kết luận )
Đọc tiếp
Bài 1: Cho ΔABC vuông tại A, phân giác BE của góc B (E ∈ AC). Từ E kẻ ED ⊥ BC (D thuộc BC). Đường thẳng BE cắt tia BA tại F
a) Chứng minh rằng ΔEAB = ΔEDB
b) Chứng minh rằng EC = EF
( Vẽ hình, viết giả thiết kết luận )
Bài 2: Cho ΔABC có AB = AC. Gọi M là trung điểm của BC
a) Chứng minh ΔABM = ΔACM
b) Chứng minh AM ⊥ BC
c) Chứng minh AM là phân giác của góc BAC
( Vẽ hình, viết giả thiết kết luận )
Bài 2:
a: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
Do đó: ΔABM=ΔACM
b: ΔAMB=ΔAMC
=>\(\widehat{AMB}=\widehat{AMC}\)
mà \(\widehat{AMB}+\widehat{AMC}=180^0\)(hai góc kề bù)
nên \(\widehat{AMB}=\widehat{AMC}=\dfrac{180^0}{2}=90^0\)
=>AM\(\perp\)BC
c: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là phân giác của \(\widehat{BAC}\)
Bài 1:
a: XétΔBAE vuông tại A và ΔBDE vuông tại D có
BE chung
\(\widehat{ABE}=\widehat{DBE}\)
Do đó: ΔBAE=ΔBDE
b: ΔBAE=ΔBDE
=>EA=ED
Xét ΔEAF vuông tại A và ΔEDC vuông tại D có
EA=ED
\(\widehat{AEF}=\widehat{DEC}\)
Do đó: ΔEAF=ΔEDC
=>EF=EC
Đúng 1
Bình luận (0)
Câu 16 : Cho tam giác ABC vuông tại A có B = 60 ° . Trên BC lấy điểm H sao cho HB =BA, từ H kẻ HE vuông góc với BC tại H, (E thuộc AC)
a/ Tính số đo góc C.
b) Chứng minh BE là tia phân giác góc B.
c) Gọi K là giao điểm của BA và HE. Chứng minh rằng BE vuông góc với KC
d/ Khi tam giác ABC có BC = 2AB Tính số đo góc B
a: goc C=90-60=30 độ
b: Xét ΔBAE vuông tại A và ΔBHE vuông tại H có
BE chung
BA=BH
=>ΔBAE=ΔBHE
=>góc ABE=góc HBE
=>BE là phân giác của góc ABC
c: Xét ΔBKC có
KH,CA là đường cao
KH cắt CA tại E
=>E là trực tâm
=>BE vuông góc KC
Đúng 0
Bình luận (0)
Cho tam giác ABC nhọn có AD và BE là hai đường cao cắt nhau tại H a, Chứng minh rằng: AD + BE < BC + AC b, Cho biết: AC < BC. Chứng minh rằng: HA < HB và AC + BE < BC + AD
a: ΔADC vuông tại D
=>AD<AC
ΔBEC vuông tại E
=>BE<BC
=>AD+BE<BC+AC
b: CA<CB
=>góc CAB>gócCBA
=>90 độ-góc CAB<90 độ-góc CBA
=>góc HBA<góc HAB
=>HA<HB
Đúng 0
Bình luận (0)