Cho điểm A cách đường thẳng xy là 12cm. Vẽ đường tròn (A ; 13cm). Chứng minh rằng đường tròn (A) có hai giao điểm với đường thẳng xy

Những câu hỏi liên quan
Cho điểm A cách đường thẳng xy là 12cm. Vẽ đường tròn (A; 13cm) :
a) Chứng minh rằng đường tròn (A) có hai giao điểm với đường thẳng xy
b) Gọi hai giao điểm nói trên là B và C. Tính độ dài BC ?
Cho điểm A cách đường thẳng xy là 12cm. Vẽ đường tròn (A ; 13cm). Gọi hai giao điểm nói trên là B và C. Tính độ dài BC.
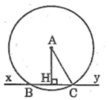
Áp dụng định lí Pitago vào tam giác vuông AHC ta có:
A C 2 = A H 2 + H C 2
Suy ra: H C 2 = A C 2 - A H 2 = 13 2 - 12 2 = 25 => HC = 5 (cm)
Ta có: BC = 2.HC = 2.5 = 10 (cm)
Đúng 0
Bình luận (0)
Cho đường tròn (O;R) và đường thẳng xy cách tâm O một khoảng OKa(0aR). Từ một điểm A thuộc xy (OAR), vẽ hai tiếp tuyến AB và AC đến đường tròn (O) (B,C là các tiếp điểm ; O và B nằm cùng phía với xy)a. Chứng minh đường thẳng xy cắt đường tròn (O) tại hai điểm D và Eb. Chứng minh 5 điểm O ,A, ,B, C, K cùng nằm trên một đường tròn. Xác định tâm của đường tròn nàyc.BC cách OA và OK theo thứ tự tại M và S. Chứng minhtuws giác AMKS nội tiếp được trong một đường tròn
Đọc tiếp
Cho đường tròn (O;R) và đường thẳng xy cách tâm O một khoảng OK=a(0<a<R). Từ một điểm A thuộc xy (OA>R), vẽ hai tiếp tuyến AB và AC đến đường tròn (O) (B,C là các tiếp điểm ; O và B nằm cùng phía với xy)
a. Chứng minh đường thẳng xy cắt đường tròn (O) tại hai điểm D và E
b. Chứng minh 5 điểm O ,A, ,B, C, K cùng nằm trên một đường tròn. Xác định tâm của đường tròn này
c.BC cách OA và OK theo thứ tự tại M và S. Chứng minhtuws giác AMKS nội tiếp được trong một đường tròn
Cho điểm M cách đường thẳng xy là 6cm. Vẽ đường tròn (M, 10cm)
a, C/m rằng đtron (M) có 2 giao điểm với đường thẳng xy
b, Gọi 2 giao điểm nói trên là P, Q. Tính độ dài PQ
a: Kẻ MH vuông góc xy tại H, gọi AB là đường kính của (M)
d(M;xy)=6cm
=>MH=6cm
AB là đường kính của (M)
=>MA=MB=10cm và AB=2*10=20(cm)
Vì MH<MA
nên xy là cát tuyến của (M)
=>(M) cắt xy tại 2 giao điểm
b:
P,Q là 2 giao điểm của (M) với xy
=>MP=MQ=10cm
ΔMPQ cân tại M
mà MH là đường cao
nên H là trung điểm của PQ
ΔMHP vuông tại H
=>\(MP^2=MH^2+HP^2\)
=>\(HP^2=10^2-6^2=64\)
=>HP=8(cm)
H là trung điểm của PQ
=>\(PQ=2\cdot PH=16\left(cm\right)\)
Đúng 2
Bình luận (0)
Cho đường thẳng xy và đường tròn (O) không giao nhau vẽ OH vuông góc với xy (H € xy ). Từ điểm A trên đường thẳng xy vẽ tiếp tuyến AB với đường tròn (B tiếp điểm). Vẽ các tuyến AMN sao cho AB và MN nằm trên hai nửa mặt phẳng bờ AO. Gọi D là trung điểm của MN. a) Chứng minh tứ giác ABOD nội tiếp b) Chứng minh AB²= AM.AN
a: ΔOMN cân tại O có OD là trung tuyến
nên OD vuông góc NA
góc ODA=góc OBA=90 độ
=>ODBA nội tiếp
b; Xét ΔABM và ΔANB có
góc ABM=góc ANB
góc BAM chung
=>ΔABM đồng dạng với ΔANB
=>AB/AN=AM/AB
=>AB^2=AN*AM
Đúng 0
Bình luận (0)
Cho đường tròn (O;3) và đường thẳng xy sao cho khoảng cách OH từ O tới xy là 4,5. Trên đường thẳng xy lấy điểm A bất kì. Từ A vẽ các tiếp tuyến AB, AC với đường tròn( B,C là các tiếp điểm). Dây BC cắt OA tại K và cắt OH tại I . CMR:
a) Tam giác AOH đồng dạng vs tam giác IOK
b) Khi A di động trên xy thì dây BC luôn đi qua 1 điểm cố định
a/ Xét tg vuông AOH và tg vuông IOK có
\(OI\perp AH;KI\perp AO\Rightarrow\widehat{KIO}=\widehat{HAO}\)
\(\Rightarrow\Delta AOH\) đồng dạng với \(\Delta IOK\)(Hai tg vuông có hai góc nhọn tương ứng bằng nhau) (1)
b/
Từ (1) \(\Rightarrow\frac{OK}{OH}=\frac{OI}{OA}\Rightarrow OH.OI=OK.OA\)
Ta có \(OA\perp BC\)(Hai tiếp tuyến xuất phát từ 1 điểm ngoài đường tròn thì đường thẳng nối điểm đó với tâm vuông góc và chia đôi dây cung tạo bởi hai tiếp điểm)
Xét tg vuông ABO có \(OB^2=OK.OA=3\) không đổi
\(\Rightarrow OH.OI\)không đổi mà OH không đổi => OI không đổi
Mà H; O cố định => I cố định => Khi A chay trên xy thì BC luôn đi qua điểm I cố định
Đúng 1
Bình luận (0)
Hai điểm A và B thuộc cùng một nửa mặt phẳng có bờ là đường thẳng xy. Khoảng cách từ điểm A đến đường thẳng xy bằng 12cm, khoảng cách từ điểm B đến xy bằng 20cm. Tính khoảng cách từ trung điểm C của AB đến xy.
Cho đường tròn (O) và điểm A cố định trên đường tròn. Gọi xy là tiếp tuyến với đường tròn tại A. Từ một điểm M nằm trên xy, vẽ tiếp tuyến MB với đường tròn. Gọi H là trực tâm của tam giác MAB. Chứng minh rằng ba điểm M, H, O thẳng hàng.
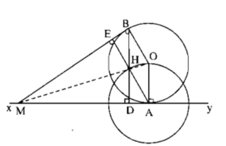
Gọi BD, AE là đường cao của ∆ MAB. Ta có ΔMAE = ∆ MBD (cạnh huyền – góc nhọn) nên ME = MD, ∆ MHE = ∆ MHD (cạnh huyền – cạnh góc vuông) nên ∠ (EMH) = ∠ (DMH). MH và MO đều là tia phân giác của góc AMB nên M, H, O thẳng hàng.
Đúng 1
Bình luận (0)
Cho điểm A nằm ngoài đường thẳng xy và cách đường thẳng xy là 3cm. Gọi M là điểm đi động trên xy. Vẽ tam giác ABC vuông tại A sao cho AM là đường cao. Tính GTNN của MB.MC


















