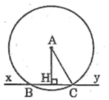
Kẻ AH ⊥ xy
Ta có: AH = 12cm
Bán kính đường tròn tâm I là 13cm nên R = 13cm
Mà AH = d = 12cm
Nên suy ra d < R
Vậy (A; 13cm) cắt đường thẳng xy tại hai điểm phân biệt B và C

Kẻ AH ⊥ xy
Ta có: AH = 12cm
Bán kính đường tròn tâm I là 13cm nên R = 13cm
Mà AH = d = 12cm
Nên suy ra d < R
Vậy (A; 13cm) cắt đường thẳng xy tại hai điểm phân biệt B và C
Cho điểm A cách đường thẳng xy là 12cm. Vẽ đường tròn (A ; 13cm). Gọi hai giao điểm nói trên là B và C. Tính độ dài BC.
Cho điểm A cách đường thẳng xy là 12 cm
a, Chứng minh (A; 13cm) cắt đường thẳng xy tại hai điểm phân biệt
b, Gọi hai giao điểm của (A; 13 cm) với xy là B, C. Tính độ dài đoạn thẳng BC.
Cho đường tròn (O) và đường thẳng xy tiếp xúc với đường tròn tại A. Vẽ đường tròn (I) đường kính OA.
a) Chứng minh rằng hai đường tròn (O) và (I) tiếp xúc với nhau
b) Vẽ dây cung AC của (O) cắt I tại một điểm thứ hai là M. Chứng minh MA=MC
c) đường thẳng OM cắt xy tại B. Chứng minh rằng BC là tiếp tuyến của (O)
Cho điểm M cách đường thẳng xy là 6cm. Vẽ đường tròn (M, 10cm)
a, C/m rằng đtron (M) có 2 giao điểm với đường thẳng xy
b, Gọi 2 giao điểm nói trên là P, Q. Tính độ dài PQ
Cho đường tròn (O) và điểm A cố định trên đường tròn. Gọi xy là tiếp tuyến với đường tròn tại A. Từ một điểm M nằm trên xy, vẽ tiếp tuyến MB với đường tròn. Gọi H là trực tâm của tam giác MAB. Chứng minh rằng ba điểm M, H, O thẳng hàng.
Cho đường tròn (O) và đường thẳng xy không có điểm chung với đường tron f(O). Gọi A là hình chiếu của O trên đường thẳng xy. Qua A vẽ cát tuyến không đi qua O cắt đường tròn tại hai điểm B và C (AB < AC). Tiếp tuyến của đường tròn tại hai điểm B và C cắt đường thẳng xy lần lượt taiij M và N.
a) Chứng minh tứ giác ABOM nội tiếp.
b) Chứng minh góc BCO bằng góc ANO và tam giác OMN cân.
c) Giả sử đường tròn (O) và đường thẳng xy cố định. Từ M vẽ tiếp tuyến thứ hai ME với đường tròn (O), E là tiếp điểm khác B. Chứng minh khi cát tuyến ABC di chuyển quanh A thì BE luôn đi qua một điểm cố định.
GIÚP MÌNH CÂU C VỚI!!!
1. Cho đường tròn ( O) và đường thẳng xy nằm ngoài đường tròn. Từ O kẻ OA vuông góc với xy. Qua A vẽ cát tuyến cắt đường tròn (O) ở B và C. Tiếp tuyến với đường tròn (O) tại B và C cắt xy ở D và E. Chứng minh: A là trung điểm của DE
2. Cho tứ giác ABCD có AB = BD nội tiếp đường tròn (O) . Từ A vẽ tiếp tuyến với đường tròn (O) cắt đường thẳng BC ở Q , gọi R là giao điểm của AB và CD. Chứng minh:
a) tứ giác AQRC nội tiếp được 1 đường tròn
b) QR//AD
Cho đường tròn (O; R) và đường thẳng xy không có điểm chung với đường tròn. Lấy một điểm A bất kỳ thuộc xy. Từ A kẻ tiếp tuyến AB với đường tròn (O) (B là tiếp điểm). Ọua B kẻ đường thẳng vuông góc với AO, cát AO tại K và cắt đường tròn (O) tại điểm thứ hai là c.
a) Tính độ dài OK nếu R = 5cm, OA = 10 cm.
b) Chứng minh ràng: AC là tiếp tuyến của đường tròn (O).
c) Kẻ OH vuông góc với xy tại H, BC cắt OH tại I. Chứng minh rằng: Khi A di chuyển trên đường thẳng xy thì độ dài đoạn thẳng OI không đổi.
Cho đường tròn (O;R) đường kính AB cố định, đường thẳng xy là tiếp tuyến của đường tròn tại B. Từ một điểm M bất kì thuộc đường tròn, kẻ đường kính MN. Gọi C, D lần lượt là giao điểm của đường thẳng AM, AN với đường thẳng xy.
a) Chứng minh tam giác NAM vuông và BC. BD = 4R^2
b) Chứng minh tứ giác CDNM nội tiếp.
c) Gọi H là trực tâm của tam giác MCD, chứng minh khi M thay đổi trên đường tròn (O) thì H thuộc một đường tròn cố định.