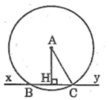
Áp dụng định lí Pitago vào tam giác vuông AHC ta có:
A C 2 = A H 2 + H C 2
Suy ra: H C 2 = A C 2 - A H 2 = 13 2 - 12 2 = 25 => HC = 5 (cm)
Ta có: BC = 2.HC = 2.5 = 10 (cm)

Áp dụng định lí Pitago vào tam giác vuông AHC ta có:
A C 2 = A H 2 + H C 2
Suy ra: H C 2 = A C 2 - A H 2 = 13 2 - 12 2 = 25 => HC = 5 (cm)
Ta có: BC = 2.HC = 2.5 = 10 (cm)
Cho điểm A cách đường thẳng xy là 12 cm
a, Chứng minh (A; 13cm) cắt đường thẳng xy tại hai điểm phân biệt
b, Gọi hai giao điểm của (A; 13 cm) với xy là B, C. Tính độ dài đoạn thẳng BC.
Cho điểm A cách đường thẳng xy là 12cm. Vẽ đường tròn (A ; 13cm). Chứng minh rằng đường tròn (A) có hai giao điểm với đường thẳng xy
Cho điểm M cách đường thẳng xy là 6cm. Vẽ đường tròn (M, 10cm)
a, C/m rằng đtron (M) có 2 giao điểm với đường thẳng xy
b, Gọi 2 giao điểm nói trên là P, Q. Tính độ dài PQ
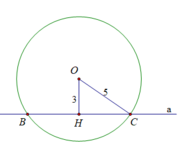
Cho đường thẳng a và có một điểm O cách a là 3cm. Vẽ đường tròn tâm O bán kính 5cm.
Gọi B và C là các giao điểm của đường thẳng a và đường tròn (O). Tính độ dài BC.
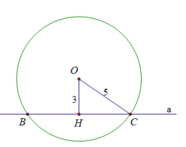
Cho đường thẳng a và có một điểm O cách a là 3cm. Vẽ đường tròn tâm O bán kính 5cm.
a) Đường thẳng a có vị trí như thế nào đối với đường tròn (O) ? Vì sao ?
b) Gọi B và C là các giao điểm của đường thẳng a và đường tròn (O). Tính độ dài BC.
a) Vẽ đồ thị hai hàm số sau trên cùng một mặt phẳng tọa độ:
y = 0,5x + 2 (1); y = 5 – 2x (2)
b) Gọi giao điểm của các đường thẳng y = 0,5x + 2 và y = 5 – 2x với trục hoành theo thứ tự là A, B và gọi giao điểm của hai đường thẳng đó là C.
Tìm tọa độ của các điểm A, B, C.
c) Tính độ dài các đoạn thẳng AB, AC và BC (đơn vị đo trên các trục tọa độ là xentimet) (làm tròn đến chữ số thập phân thứ hai).
d) Tính các góc tạo bởi các đường thẳng có phương trình (1) và (2) với trục Ox (làm tròn đến phút).
cho nửa đường tròn tâm O đường kính AB=2x (x là một độ dài cho trước) Gọi C,D là hai điểm trên nửa đường tròn đó sao cho C thuộc cung AD và góc COD= 120 độ , Gọi giao điểm của hai dây AD và BC là E, giao điểm của hai đường thẳng AC và BD là F
a) cmr bốn điểm C, D,E,F cùng nằm trên một đường tròn
b) TÍnh bán kính của đường tròn đi qua C, E, D, F nói trên theo x
c) Tìm GTLN của diện tích tam giác FAB theo R khi C, D thay đổi nhưng vẫn thỏa mãn giả thiết
Cho đường thẳng xy và một điểm A cắt xy tại một khoảng bằng 6cm. Vì tâm A có bán kính 10cm
a) CMR có 2 giao điểm với đường tròn tâm A
b) Gọi hai giao điểm trên là B, C. Tính BC?
Cho đường tròn (O;R) đường kính AB. Trên tiếp tuyến tại A của (O;R) lấy điểm C sao cho AC = 2R. Gọi D là giao điểm của BC và đường tròn (O)
a) CM: AD là đường cao và cũng là đường trung tuyến của ΔABC
b) Vẽ dây cung AE vuông góc với OC tại H. CM:CE là tiếp tuyến của đường tròn (O;R)
c) Đường thẳng BE cắt đường thẳng OD tại F. Tính tanOBF và suy ra số độ của góc OFB
d) Gọi K là hình chiếu của điểm E xuống AB, M là giao điểm của EK với BC. Tính độ dài các đoạn thẳng ME và MK theo R