Giả sử x 1 , x 2 là hai nghiệm của phương trình 3 x + 4 = 9 x 2 − 3 x , x 1 < x 2 . Tính giá trị biểu thức P = 2 x 1 + x 2
A. 3
B. 0
C. 2
D. 1
Cho hệ phương trình x + y + 1 + 1 = 4 x + y 2 + 3 . x + y 2 x - y = 3 2 .Giả sử (x;y) là cặp nghiệm của hệ phương trình. Khi đó, A = 9x2 – 12y + 1 bằng
A. 3
B. 9
C. 4
D. 7
Giả sử ∫ 2 x + 3 x ( x + 1 ) ( x + 2 ) ( x + 3 ) + 1 d x = - 1 g ( x ) + C (C là hằng số). Tính tổng của các nghiệm của phương trình g(x) = 0
A. –1
B. 1
C. 3
D. –3
Đáp án D
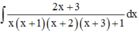
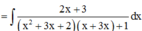
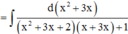
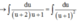
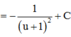
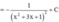
Suy ra tổng của các nghiệm của phương trình g(x) = 0 là - 3
Giả sử ∫ 2 x + 3 x ( x + 1 ) ( x + 2 ) ( x + 3 ) + 1 d x = - 1 g ( x ) + C (C là hằng số). Tính tổng của các nghiệm của phương trình g(x) = 0
A. -1
B. 1
C. 3
D. -3
Cho hệ phương trình 5 x + 2 y = - 3 3 x + y = - 2
Giả sử (x;y) là nghiệm của hệ phương trình, khi đó - x . y 3 bằng
A. -1.
B. 1
C. 2
D. -2
2. Cho phương trình x^2 + mx + m - 1 (m là tham số). (1)
a) Giải phương trình khi m = 5
b) Chứng minh phương trình (1) luôn có nghiệm với mọi giá trị của m. Giả sử x1,x2 là hai nghiệm của phương trình (1), tìm giá trị nhỏ nhất của biểu thức: Q = x1^2 + x2^2 = 4x1 - 4x2.
a: Khi m=5 thì (1) sẽ là: x^2+5x+4=0
=>x=-1; x=-4
b: Sửa đề: Q=x1^2+x2^2-4x1-4x2
Q=(x1+x2)^2-2x1x2-4(x1+x2)
=m^2-2(m-1)-4(-m)
=m^2-2m+2+4m
=m^2+2m+2=(m+1)^2+1>=1
Dấu = xảy ra khi m=-1
Cho phương trình A x 3 + 2 C x + 1 x - 1 - 3 C x - 1 x - 3 = 3 x 2 + P 6 + 159 Giả sử x = x0 là nghiệm của phương trình trên, lúc này ta có
A. x0 ∈(10;13)
B. x0 ∈(12;14)
C. x0 ∈(10;12)
D. x0 ∈(14;16).
Điều kiện x ≥ 3, x ∈ N. Phương trình đã cho có dạng:
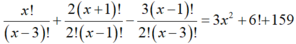
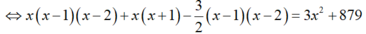
Suy ra x=12.
Chọn B.
Giả sử phương trình bậc hai ẩn x (m là tham số): \(x^2-2\left(m-1\right)x-m^3+\left(m+1\right)^2=0\\ \)
có hai nghiệm x1,x2 thỏa mãn điều kiện \(x_1+x_2\le4\). Tìm giá trị lớn nhất và nhỏ nhất của biểu thức sau:
\(P=x^3_1+x_2^3+x_1x_2\left(3x_1+3x_2+8\right)\)
\(\Delta'=\left(m-1\right)^2+m^3-\left(m+1\right)^2=m^3-4m\ge0\) \(\Rightarrow\left[{}\begin{matrix}m\ge2\\-2\le m\le0\end{matrix}\right.\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2\left(m-1\right)\\x_1x_2=-m^3+\left(m+1\right)^2\end{matrix}\right.\)
Do \(x_1+x_2\le4\Rightarrow m-1\le2\Rightarrow m\le3\)
\(\Rightarrow\left[{}\begin{matrix}2\le m\le3\\-2\le m\le0\end{matrix}\right.\)
\(P=x_1^3+x_2^3+3x_1x_2\left(x_1+x_2\right)+8x_1x_2\)
\(=\left(x_1+x_2\right)^3+8x_1x_2\)
\(=8\left(m-1\right)^3+8\left[-m^3+\left(m+1\right)^2\right]\)
\(=8\left(5m-2m^2\right)\)
\(P=8\left(5m-2m^2-2+2\right)=16-8\left(m-2\right)\left(2m-1\right)\le16\)
\(P_{max}=16\) khi \(m=2\)
\(P=8\left(5m-2m^2+18-18\right)=8\left(9-2m\right)\left(m+2\right)-144\ge-144\)
\(P_{min}=-144\) khi \(m=-2\)
giả sử a,b là nghiệm của phương trình \(x^2+px+1=0\)
giả sử c,d là nghiệm của phương trình \(x^2+qx+1=0\)
chứng minh hệ thức: (a-c)(a+d)(b+d)=\(q^2-p^2\)
Cho phương trình A x 3 + 2 C x + 1 x - 1 - 3 C x - 1 x - 3 = 3 x 2 + P 6 + 159 Giả sử x = x 0 là nghiệm của phương trình trên, khi đó
A. x 0 ∈ 10 ; 13
B. x 0 ∈ 10 ; 12
C. x 0 ∈ 12 ; 14
D. x 0 ∈ 14 ; 16
Cho hệ phương trình - x + 2 y - 3 z = 2 6 x - y + 3 z = - 3 - 2 x - 3 y + z = 2
Giả sử (x; y;z) là nghiệm của hệ phương trình. Trong các khẳng định sau, khẳng định đúng là
![]()
![]()
![]()
![]()