Điều kiện x ≥ 3, x ∈ N. Phương trình đã cho có dạng:
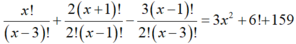
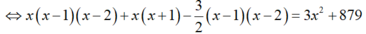
Suy ra x=12.
Chọn B.
Điều kiện x ≥ 3, x ∈ N. Phương trình đã cho có dạng:
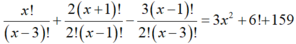
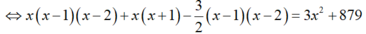
Suy ra x=12.
Chọn B.
Cho phương trình A x 3 + 2 C x + 1 x - 1 - 3 C x - 1 x - 3 = 3 x 2 + P 6 + 159 Giả sử x = x 0 là nghiệm của phương trình trên, khi đó
A. x 0 ∈ 10 ; 13
B. x 0 ∈ 10 ; 12
C. x 0 ∈ 12 ; 14
D. x 0 ∈ 14 ; 16
Cho phương trình A x 3 + 2 C x + 1 x - 3 - 3 C x - 1 x - 3 = 3 x 2 + P 6 + 159 . Giả sử x = x 0 là nghiệm của phương trình trên, khi đó
![]()
![]()
![]()
![]()
Cho hàm số y= f(x)=x^3-2x^2 (C) a) Tìm f'(x). Giải bất phương trình f'(x)>0 b) Viết phương trình tiếp tuyến của (C) tại điểm M có hoành độ x0=2
Cho hàm số y = f(x)=x^3-2x^2(C) a) tìm f'(x) . Giải bất phương trình f'(x)>0 b) viết phương trình tiếp tuyến của (C) tại điểm M có hoành độ x0=2
Chứng minh rằng phương trình x 3 + x - 1 = 0 có nghiệm duy nhất x 0 thỏa mãn 0 < x 0 < 1 2
Cho các hàm số
f ( x ) = x 3 + b x 2 + c x + d ( C )
g ( x ) = x 2 − 3 x − 1 .
a) Xác định b, c, d sao cho đồ thị (C) đi qua các điểm (1; 3), (−1; −3) và f′(1/3) = 5/3 ;
b) Viết phương trình tiếp tuyến của (C) tại điểm có hoành độ x 0 = 1 ;
c) Giải phương trình f′(sint) = 3;
d) Giải phương trình f′′(cost) = g′(sint);
e) Tìm giới hạn lim z → 0 f ' ' sin 5 z + 2 g ' sin 3 z + 3
Viết phương trình tiếp tuyến của:
a) Hypebol y = x + 1 x - 1 tại điểm A 2 ; 3 .
b) Đường cong y = x 3 + 4 x 2 – 1 tại điểm có hoành độ x 0 = - 1 .
c) Của parabol y = x 2 – 4 x + 4 tại điểm có tung độ y 0 = 1 .
Cho hàm số y = f(x) xác định trên khoảng (a; b) chứa điểm x 0
Chứng minh rằng nếu lim x → x 0 f ( x ) - f ( x 0 ) x - x 0 = L thì hàm số f(x) liên tục tại điểm x 0
Đặt g ( x ) = f ( x ) - f ( x 0 ) x - x 0 - L và biểu diễn f(x) qua g(x)
Cho hàm số y = sin4x
a) Chứng minh rằng sin4(x + kπ/2) = sin4x với k ∈ Z
Từ đó vẽ đồ thị của hàm số
y = sin4x; (C1)
y = sin4x + 1. (C2)
b) Xác định giá trị của m để phương trình: sin4x + 1 = m (1)
- Có nghiệm
- Vô nghiệm
c) Viết phương trình tiếp tuyến của (C2) tại điểm có hoành độ x 0 = π / 24