Trên một đường tròn, lấy liên tiếp ba cung AC,CD, DB sao chosđ A C ⏜ = sđ C D ⏜...

Hãy tham gia nhóm Học sinh Hoc24OLM

Bạn chưa đăng nhập. Vui lòng đăng nhập để hỏi bài

Chọn lớp:

Chọn môn:

Gửi câu hỏi ẩn danh

Pham Trong Bach 17 tháng 8 2018 lúc 9:12

Trên một đường tròn, lấy liên tiếp ba cung AC,CD, DB sao chosđ A C ⏜ sđ C D ⏜ sđ D B ⏜ 60 o Hai đường thẳng AC và DB cắt nhau tại E. Hai tiếp tuyến của đường tròn tại B và C cắt nhau tại T. Chứng minh rằng:CD là tia phân giác của B C...

Đọc tiếp

Trên một đường tròn, lấy liên tiếp ba cung AC,CD, DB sao cho

sđ A C ⏜ = sđ C D ⏜ = sđ D B ⏜ = 60 o

Hai đường thẳng AC và DB cắt nhau tại E. Hai tiếp tuyến của đường tròn tại B và C cắt nhau tại T. Chứng minh rằng:

CD là tia phân giác của B C T ^

Lớp 9 Toán

Những câu hỏi liên quan

Pham Trong Bach

18 tháng 11 2017 lúc 5:07

Đọc tiếp

Trên một đường tròn, lấy liên tiếp ba cung AC,CD, DB sao cho

sđ A C ⏜ = sđ C D ⏜ = sđ D B ⏜ = 60 o

Hai đường thẳng AC và DB cắt nhau tại E. Hai tiếp tuyến của đường tròn tại B và C cắt nhau tại T. Chứng minh rằng:

A E B ^ = B T C ^

Xem chi tiết

Lớp 9 Toán

Cao Minh Tâm

18 tháng 11 2017 lúc 5:09

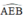Giải bài 38 trang 82 SGK Toán 9 Tập 2 | Giải toán lớp 9

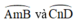
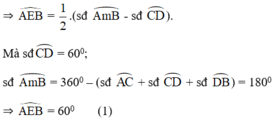
a) + Giải bài 38 trang 82 SGK Toán 9 Tập 2 | Giải toán lớp 9 là góc có đỉnh ở ngoài đường tròn chắn hai cung

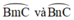
Giải bài 38 trang 82 SGK Toán 9 Tập 2 | Giải toán lớp 9

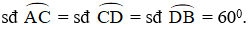
+ Giải bài 38 trang 82 SGK Toán 9 Tập 2 | Giải toán lớp 9 là góc có đỉnh ở ngoài đường tròn chắn hai cung

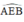Giải bài 38 trang 82 SGK Toán 9 Tập 2 | Giải toán lớp 9

Đúng 0

Bình luận (0)

Hoàng Minh Lê

7 tháng 3 2022 lúc 16:14

Trên một đường tròn, lấy liên tiếp ba cung AC,CD, DB sao cho Hai đường thẳng AC và DB cắt nhau tại E. Hai tiếp tuyến của đường tròn tại B và C cắt nhau tại T. Chứng minh rằng:

Đọc tiếp

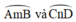
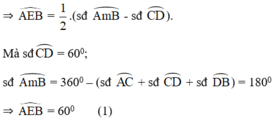
Trên một đường tròn, lấy liên tiếp ba cung AC,CD, DB sao cho Giải bài 38 trang 82 SGK Toán 9 Tập 2 | Giải toán lớp 9 Hai đường thẳng AC và DB cắt nhau tại E. Hai tiếp tuyến của đường tròn tại B và C cắt nhau tại T. Chứng minh rằng:

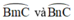
Giải bài 38 trang 82 SGK Toán 9 Tập 2 | Giải toán lớp 9

Xem chi tiết

Lớp 9 Toán Bài 5: Góc có đỉnh bên trong đường tròn. Góc có đỉ...

Pham Trong Bach

17 tháng 3 2018 lúc 2:02

Trên một đường tròn, lấy liên tiếp ba cung AC,CD, DB sao cho sd AC ^ sd CD → sd DB ^ 60 ° Hai đường thẳng AC và DB cắt nhau tại E. Hai tiếp tuyến của đường tròn tại B và C cắt nhau tại T. Chứng minh rằng:a). AEB ^ BTC ^ b) CD là tia phân giác của góc BCT

Đọc tiếp

Trên một đường tròn, lấy liên tiếp ba cung AC,CD, DB sao cho

sd AC ^ = sd CD → = sd DB ^ = 60 °

Hai đường thẳng AC và DB cắt nhau tại E. Hai tiếp tuyến của đường tròn tại B và C cắt nhau tại T. Chứng minh rằng:

a). AEB ^ = BTC ^

b) CD là tia phân giác của góc BCT

Xem chi tiết

Lớp 9 Toán

Cao Minh Tâm

17 tháng 3 2018 lúc 2:03

Giải bài 38 trang 82 SGK Toán 9 Tập 2 | Giải toán lớp 9

a) + Giải bài 38 trang 82 SGK Toán 9 Tập 2 | Giải toán lớp 9 là góc có đỉnh ở ngoài đường tròn chắn hai cung

Giải bài 38 trang 82 SGK Toán 9 Tập 2 | Giải toán lớp 9

+ Giải bài 38 trang 82 SGK Toán 9 Tập 2 | Giải toán lớp 9 là góc có đỉnh ở ngoài đường tròn chắn hai cung

Giải bài 38 trang 82 SGK Toán 9 Tập 2 | Giải toán lớp 9

b) Giải bài 38 trang 82 SGK Toán 9 Tập 2 | Giải toán lớp 9 là góc tạo bởi tiếp tuyến CT và dây CD

Giải bài 38 trang 82 SGK Toán 9 Tập 2 | Giải toán lớp 9

Kiến thức áp dụng

+ Số đo của góc có đỉnh ở bên ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn.

Đúng 0

Bình luận (0)

Bài 38

SGK trang 82

11 tháng 4 2017 lúc 11:25

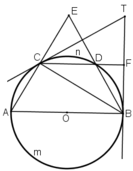
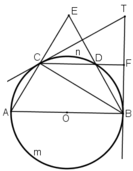
Trên một đường tròn, lấy liên tiếp ba cung AC, CD, DB sao cho số đo cung AC bằng số đo cung CD bằng số đo cung DB và bằng 60^o. Hai đường thẳng AC và BD cắt nhau tại E. Hai tiếp tuyến của đường tròn tại B và C cắt nhau tại T. Chứng minh rằng:

a) \(\widehat{AEB}=\widehat{BTC}.\)

b) CD là tia phân giác của \(\widehat{BCT}.\)

Xem chi tiết

Lớp 9 Toán Bài 5: Góc có đỉnh bên trong đường tròn. Góc có đỉ...

Quốc Đạt

11 tháng 4 2017 lúc 11:50

a) Ta có 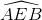là góc có đỉnh ở bên ngoài đường tròn nên:

\(\widehat{AEB}=\dfrac{sđ\left(\widehat{AB}-\widehat{CD}\right)}{2}=\dfrac{180^O-60^O}{2}=60^O\)

và \(\widehat{BTC}\) cũng là góc có đỉnh ở bên ngoài đường tròn ( hai cạnh đều là tiếp tuyến của đường tròn) nên:

\(\widehat{BTC}\) = sđ\(\dfrac{\widehat{BAC}-\widehat{BDC}}{2}=\dfrac{\left(180^O+60^O\right)-\left(60^O+60^O\right)}{2}=60^O\)

Vậy =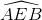

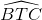
b) \(\widehat{DCT}\) là góc tạo bởi tiếp tuyến và dây cung nên:

\(\widehat{DCT}=\dfrac{sđ\widehat{CD}}{2}=\dfrac{60^o}{2}=30^o\)

→ \(\widehat{DCB}\) là góc nội tiếp trên

\(\widehat{DCB}\) = \(\dfrac{sđ\widehat{DB}}{2}\) = \(\dfrac{60^O}{2}=30^O\)

Vậy \(\widehat{DCT}\) = \(\widehat{DCB}\) hay CD là phân giác của \(\widehat{BCT}\)

Đúng 0

Bình luận (0)

Ly thị sát

16 tháng 3 2023 lúc 7:58

Trên đường tròn lấy liên tiếp 3 cung AC ,CD,DB sao cho số đo của cung AC bằng số đo của cung góc AC = số đo của cung góc CD =60° hai đường thẳng AC và BD cắt nhau tại E hai tiếp tuyến của đường tròn tại B và C cắt nhau tại T chứ minh rằng a, góc AEB = góc BTC. b, CD là tia phân giác của góc BTC M.n giúp em với ạ

Xem chi tiết

Lớp 9 Toán

Nguyễn Lê Phước Thịnh CTV

16 tháng 3 2023 lúc 8:12

a: Xét ΔOAC có OA=OC và góc AOC=60 độ

nên ΔOAC đều

=>góc CAO=60 độ

Xet ΔOBD có OB=OD và góc DOB=60 độ

nên ΔOBD đều

=>góc B=60 độ

Xét ΔEAB có góc EAB=góc EBA=60 độ

nên ΔEAB đều

=>góc E=60 độ

góc BOC=60+60=120 độ

=>góc BTC=60 độ=góc AEB

Đúng 0

Bình luận (0)

Nguyenn Nguyenn

27 tháng 4 2021 lúc 18:22

Trên đường tròn tâm O đường kính AB=2R , lấy điểm C sao cho sđ cung BC=60° . Hai tiếp tuyến với đường tròn vẽ từ B và C cắt nhau tại D .
a) Tính sđ góc BOC và sđ cung nhỏ AC .
b) chứng minh tứ giác OBDC nội tiếp .
c) Tia AC cắt tia BD tại E . Chứng minh D là trung điểm của BE .
d) Biết R=15cm . Tính diện tích hình quạt giới hạn bởi cung nhỏ AC( biết π=3,14)

Xem chi tiết

Lớp 9 Toán Ôn thi vào 10

Nguyenn Nguyenn

27 tháng 4 2021 lúc 18:23

giúp em với năn nỉ m,n

Đúng 0

Bình luận (0)

Trần Liêu Thiên Vương

27 tháng 4 2021 lúc 12:33

Trên đường tròn tâm O đường kính AB=2R , lấy điểm C sao cho sđ cung BC=60° . Hai tiếp tuyến với đường tròn vẽ từ B và C cắt nhau tại D . a) Tính sđ góc BOC và sđ cung nhỏ AC . b) chứng minh tứ giác OBDC nội tiếp . c) Tia AC cắt tia BD tại E . Chứng minh D là trung điểm của BE . d) Biết R=15cm . Tính diện tích hình quạt giới hạn bởi cung nhỏ AC( biết π=3,14)

Xem chi tiết

Lớp 9 Toán

Linh Cao Minh

19 tháng 2 2016 lúc 22:27

Cho nửa đường tròn tâm O, đường kính AB

Trên nửa đường tròn lấy 2 điểm C và D, C thuộc cung AD, sao cho sđ cung CD=90 độ

Hai tia AC, BD cắt nhau tại M.

Tìm quỹ tích M

Xem chi tiết

Lớp 9 Toán Câu hỏi của OLM

Nguyễn ngọc quỳnh lam

10 tháng 3 2019 lúc 9:11

Trên một đường tròn lấy liên tiếp 3 cung AC,CD,DB sao cho sđ stackrelfrown{AC}sđstackrelfrown{CD}sđstackrelfrown{DB}60độ. Hai đường thẳng AC và BD cắt nhau ở E. Hai tiếp tuyến của đường tròn tại B và C cắt nhau. Chứng minh rằng: a. widehat{AEB} widehat{BTC}. b. Chứng minh CD là tia phân giác của góc BCI

Đọc tiếp

Trên một đường tròn lấy liên tiếp 3 cung AC,CD,DB sao cho sđ \(\stackrel\frown{AC}\)=sđ\(\stackrel\frown{CD}\)=sđ\(\stackrel\frown{DB}\)=60^\(\)độ. Hai đường thẳng AC và BD cắt nhau ở E. Hai tiếp tuyến của đường tròn tại B và C cắt nhau. Chứng minh rằng:

a. \(\widehat{AEB}\) =\(\widehat{BTC}\).

b. Chứng minh CD là tia phân giác của góc BCI

Xem chi tiết

Lớp 9 Toán Ôn tập góc với đường tròn

Câu hỏi

Khoá học trên OLM (olm.vn)