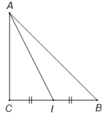
Cho tam giác ABC vuông cân đỉnh C, A B = 2 .Tính độ dài của A B → + A C →
![]()
![]()
![]()
![]()
Bài 7: a, Cho tam giác ABC vuông tại A có AB 3 AC 4 = và BC = 5. Tính độ dài AB, AC b, Tính độ dài cạnh huyền biết độ dài hai cạnh góc vuông là 6 và 7 c, Tính góc ở đỉnh của tam giác cân biết số đo góc ở đáy là 200 d, Tính số đo góc ở đáy tam giác cân biết số đo góc ở đỉnh là 600
b: Độ dài cạnh huyền là \(\sqrt{6^2+7^2}=\sqrt{85}\left(cm\right)\)
c: Số đo góc ở đỉnh là:
\(180-2\cdot20^0=140^0\)
d: Số đó góc ở đáy là:
\(\dfrac{180^0-60^0}{2}=60^0\)
Cho tam giác ABC vuông cân đỉnh C, AB = 2 . Tính độ dài của A B → + A C →
A. ![]()
B. ![]()
C. ![]()
D. ![]()
a,Tính các góc ở đáy của 1 tam giác cân biết góc ở đỉnh bằng 50 độ
b, Cho tam giác đều ABC cạnh 3cm. Gọi M là trung điểm BC. Tính độ dài AM
c, Tính các góc ở đỉnh của tam giác cân biết góc đáy = 50 độ
a) Vì là tam giác cân nên 2 góc ở đáy bằng nhau, góc ở đáy là : \(\left(180^0-50^0\right)\div2=65^0\)
b) Vì \(\Delta ABC\) đều \(\Rightarrow\widehat{A}=\widehat{B}=\widehat{C}=180^0\div3=60^0\).Có \(BM=CM=1,5\left(cm\right)\)
\(\Rightarrow\Delta ABM=\Delta ACM\left(c.c.c\right)\Rightarrow\widehat{AMC}=\widehat{AMB}\). Mà 2 góc kề bù \(\Rightarrow\widehat{AMC}=\widehat{AMB}=90^0\)
Vì \(\Rightarrow\widehat{AMB}=90^0\Rightarrow\Delta AMB\) có \(AM^2=AB^2+BM^2\). Thay số. ta có :
\\(AM^2=3^2+1,5^2=9+2,25=11,25\Rightarrow AM=\sqrt{11,25}\)
c) Vì là tam giác cân nên 2 góc ở đáy bằng nhau, góc ở đỉnh là : \(180^0-\left(50^0.2\right)=80^0\)
b) \(AM^2+MB^2=AB^2\)
\(\Rightarrow AM=\sqrt{AB^2-MB^2}=\sqrt{3^2-1,5^2}=\sqrt{6,75}\)
học lại đinhl ý pytago nha Vũ Cao Minh⁀ᶦᵈᵒᶫ ( Cool Team )
cho tam giác abc,vẽ tam giác vuông cân abd(b=90 độ sao cho a và d ở 2 phía của bc.vẽ tam giác vuông cân cbg(đỉnh b)sao cho g và a ở cùng phía vs bc .cm: ga=dc và tính góc tạo bởi ga và dc
a) Tính góc ở đỉnh của một tam giác cân biết góc ở đáy của tam giác đó bằng 50 độ
b) Tính góc ở đáy của một tam giác cân biết góc ở đỉnh của tam giác đó bằng 70 độ
c)Tam giác ABC cân tại A, tính góc B và góc C theo góc A
a) Ta có góc ở đáy của tam giác cân bằng 50 độ. Do đó tổng của hai góc đáy của tam giác cân bằng 50.2=100độ. Góc ở đỉnh bằng 180-100=80 độ
b) Ta có góc đỉnh của tam giác câ là 70 độ. Do đó mỗi góc ở đáy bằng (180-70):2=55 độ
c) góc B= góc C=(180-A):2
cho tam giác ABC có góc A=75 độ 1 đường thẳng đi qua đỉnh A và cắt BC tại M và chia tam giác ABC thành 2 tam giác cân .Tính góc B và C của tam giác ABC
Cho tam giác ABC vuông cân ở A. Biết AB=AC=4 cm
a, Tính độ dài cạnh BC
b, Từ A kẻ AD vuông góc Bc. C/m D là trung điểm của BC
c, Từ D kẻ DF vuông góc AC. C/m tam giác AFD là tam giác vuông cân
d, Tính độ dài đoạn AD
Bạn vui lòng tự vẽ hình giùm.
a) Tính độ dài BC.
Ta có \(\Delta ABC\)vuông tại A => BC2 = AB2 + AC2 (định lí Pitago) (1)
Mà AB = AC (\(\Delta ABC\)cân tại A) => AB2 = AC2 (2)
Từ (1) và (2) => BC2 = 2AB2
=> BC2 = 2. 42 = 32
=> BC = \(\sqrt{32}\)(vì BC > 0)
b) CM: D là trung điểm của BC
\(\Delta ADB\)vuông và \(\Delta ADC\)vuông có: AB = AC (\(\Delta ABC\)cân tại A)
Cạnh AD chung
=> \(\Delta ADB\)vuông = \(\Delta ADC\)vuông (cạnh huyền - cạnh góc vuông) => DB = DC (hai cạnh tương ứng) => D là trung điểm của BC (đpcm)
* Hình bạn tự vẽ xD *
a) Ta có : Tam giác ABC vuông cân tại A
=> AB2 + AC2 = BC2 ( Đ.lí Pytago )
=> 42 + 42 = BC2
=> 16 + 16 = BC2
=> 32 = BC2
=> BC = \(\sqrt{32}cm\)
b) Vì tam giác ABC là tam giác vuông cân tại A => Góc B = góc C ( hai góc ở đáy )
Xét tam giác vuông ADB và tam giác vuông ADC có :
AB = AC ( gt )
B = C ( cmt )
=> Tam giác vuông ADB = tam giác vuông ADC ( cạnh huyền - góc nhọn )
=> DB = DC ( hai cạnh tương ứng )
=> D là trung điểm của BC
( Đến đây thì mình bí r xD )
Trong mặt phẳng toạ độ, cho tam giác ABC có A(1; 0), B(3; 2) và C(-2;-1).
a) Tính độ dài đường cao kẻ từ đỉnh A của tam giác ABC.
b) Tính diện tích tam giác ABC.
a) Ta có: \(\overrightarrow {{u_{BC}}} = \overrightarrow {BC} = \left( { - 5; - 3} \right) \Rightarrow \overrightarrow {{n_{BC}}} = \left( {3; - 5} \right)\) . Vậy phương trình tổng quát của đường thẳng BC là: \(3\left( {x - 3} \right) - 5\left( {y - 2} \right) = 0 \Leftrightarrow 3x - 5y + 1 = 0\).
Độ dài đường cao AK của tam giác \(ABC\) hạ từ đỉnh A là: \(AK = d\left( {A,BC} \right) = \frac{{\left| {3.1 - 0.5 + 1} \right|}}{{\sqrt {{3^2} + {{\left( { - 5} \right)}^2}} }} = \frac{4}{{\sqrt {34} }}\)
b) Ta có: \(\overrightarrow {BC} = \left( { - 5; - 3} \right) \Rightarrow BC = \sqrt {{{\left( { - 5} \right)}^2} + {{\left( { - 3} \right)}^2}} = \sqrt {34} \)
Diện tích tam giác ABC là: \({S_{ABC}} = \frac{1}{2}.AK.BC = \frac{1}{2}.\frac{4}{{\sqrt {34} }}.\sqrt {34} = 2\)
Độ dài cạnh góc vuông của một tam giác vuông cân ABC tại A có đường phân giác kẻ từ đỉnh A bằng 3√2/2 cm là ...........cm.
a. 3b. 2c. 5d. 4ABC cân nên đpg Ah cx là đườg cao;AH=BC/2
=>BC=3căn2
ta có: AB*AC=BC*AH<=>AB^2=3căn2*3căn2/2<=>AB=3