Chọn A.
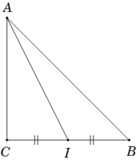
Ta có 
.Nên AC = CB = 1
Gọi I là trung điểm BC suy ra 
Khi đó 
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Cho tam giác ABC có các đỉnh A(-1;3), B(1;0) và C(2;-1). Tính độ dài đường cao của tam giác ABC vẽ từ điểm A?
A. 1
B. 2 2
C. 2
D. 3 2 2
Tính độ dài đường trung tuyến
Cho tam giác ABC, có cạnh BC=a, AC=b, AB =c. Gọi ma , mb , mc lần lượt là độ dài trung tuyến từ đỉnh A, B, C của tam giác. Hãy tính ma , mb , mc theo a, b, c.
Cho tam giác ABC có AB c; BC a; AC b . Nếu giữa a; b; c có liên hệ b2 + c2 2a2 thì độ dài đường trung tuyến xuất phát từ đỉnh A của tam giác tính theo a bằng: A.
a
3
2
B.
a
3
3
C. a D. 2a
Đọc tiếp
Cho tam giác ABC có AB = c; BC = a; AC = b . Nếu giữa a; b; c có liên hệ b2 + c2 = 2a2 thì độ dài đường trung tuyến xuất phát từ đỉnh A của tam giác tính theo a bằng:
A. a 3 2
B. a 3 3
C. a
D. 2a
Cho tam giác ABC có \(\stackrel\frown{B}\) = \(75^o\), \(\stackrel\frown{C}=45^o\) và BC = 50.
a) Tính độ dài cạnh AB.
b) Tính diện tích tam giác ABC.
c) Tính đường cao xuất phát từ đỉnh A của tam giác ABC
Cho tam giác ABC có A(1;-1); B(-1;0); C(3;3). Độ dài đường cao xuất phát từ đỉnh A của tam giác ABC bằng
A. 2
B. 3
C. 5
D. 6
Cho tam giác đều ABC có cạnh bằng 6cm. Một điểm M nằm trên cạnh BC sao cho BM = 2cm.
a, Tính độ dài của đoạn thẳng AM và tính côsin của góc BAM ;
b, Tính bán kính đường tròn ngoại tiếp tam giác ABM;
c, Tính độ dài đường trung tuyến vẽ từ đỉnh C của tam giác ACM;
d, Tính diện tích tam giác ABM.
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(2;4), trọng tâm G ( 2 ; 2 3 ) . Biết rằng đỉnh B nằm trên đường thẳng d: x + y + 2 = 0 và đỉnh C có hình chiếu vuông góc trên d là điểm H(2;-4). Giả sử B(a;b). Tính giá trị của biểu thức P = a - 3b.
Trong mpOxy, cho tam giác ABC có A(1; 1), B(3; 3), C(0;-6).
1,Tính cos A.
2,Tìm tọa độ điểm D sao cho tam giác ABD vuông cân tại D.
3,Gọi E là chân đường phân giác trong của góc A.Tìm tọa độ điểm E.
Cho tam giác ABC vuông cân tại C và
A
B
2
.
Tính độ dài của
A
B
→
+
A
C
→
.
A.
A
B
→
+
A
C
→...
Đọc tiếp
Cho tam giác ABC vuông cân tại C và A B = 2 . Tính độ dài của A B → + A C → .
A. A B → + A C → = 5 .
B. A B → + A C → = 2 5 .
C. A B → + A C → = 3 .
D. A B → + A C → = 2 3 .