Cho hình vẽ:
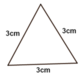
Chu vi của tam giác trên là:
A. 11cm
B. 10cm
C. 9cm
D. 8cm
Bạn cho mình hỏi chỗ :2√2 là j ạ
a) Ta có: \(\left(2\sqrt{2}\right)^2=8\)
\(2^2+2^2=4+4=8\)
Do đó: \(\left(2\sqrt{2}\right)^2=2^2+2^2\)(=8)
hay \(2\sqrt{2}\)cm; 2cm; 2cm là số đo ba cạnh của một tam giác vuông
b) Ta có: \(17^2=289\)
\(8^2+15^2=64+225=289\)
Do đó: \(17^2=8^2+15^2\)(=289)
hay 17cm; 8cm và 15cm là số đo ba cạnh của một tam giác vuông
c) Ta có: \(25^2=625\)
\(7^2+24^2=49+576=625\)
Do đó: \(25^2=7^2+24^2\)(=625)
hay 25cm; 7cm và 24cm là số đo ba cạnh của một tam giác vuông
d) Ta có: \(10^2=100\)
\(6^2+8^2=36+64=100\)
Do đó: \(10^2=6^2+8^2\)(=100)
hay 10cm; 6cm và 8cm là số đo ba cạnh của một tam giác vuông
e) Ta có: \(11^2=121\)
\(6^2+9^2=36+81=117\)
Do đó: \(11^2\ne6^2+9^2\)(\(121\ne117\))
hay 11cm; 6cm và 9cm không là số đo ba cạnh của một tam giác vuông
f) Ta có: \(\left(\dfrac{3}{2}\right)^2=\dfrac{9}{4}\)
\(1^2+1^2=1+1=2=\dfrac{8}{4}\)
Do đó: \(\left(\dfrac{3}{2}\right)^2\ne1^2+1^2\left(\dfrac{9}{4}\ne\dfrac{8}{4}\right)\)
hay \(\dfrac{3}{2}cm\); 1cm và 1cm không là số đo ba cạnh của một tam giác vuông
Bộ ba nào có thể là độ dài ba cạnh của một tam giác? A:7cm,8cm,11cm B:7cm,9cm,16cm C:8cm,9cm,16cm
`A, 7 cm, 8cm, 11 cm.`
Theo bất đẳng thức tam giác: `7+8 > 11 > 8-7`
`->` Bộ `3` độ dài này có thể là bộ ba cạnh của `1` tam giác.
`B, 7cm, 9cm, 16cm`
Theo bất đẳng thức tam giác: `7+9 = 16 > 9-7`
`->` Bộ `3` độ dài này không thể là độ dài của `1` tam giác.
`C, 8cm, 9cm, 16cm`
Theo bất đẳng thức tam giác: `8+9 > 16 > 9-8`
`->` Bộ `3` độ dài này có thể là độ dài trong `1` tam giác.
`-> A, C`
`\color{blue}\text {#DuyNam}`
Tam giác nào là tam hiacs vuông trong các tam giác có độ dài ba cạnh như sau: A.2cm; 4cm; 5cm B.7cm; 10cm; 5cm C.10cm; 9cm; 11cm D.3cm; 4cm; 5cm
Chọn D
52 = 25
32 + 42 = 9 + 16 = 25
52 =32 + 42
Vậy độ dài của 3 cạnh đó làđộ dài của 3 cạnh tam giác vuông
trong các độ dài sau ba số ào là số đo 3 cạnh của 1 tam giác vuông
A 6cm, 10cm, 8cm
B 6cm, 9cm, 11cm
giải cho mik cách lm ạ
a) Do 62+82=102 nên là tam giác vuông
b) do 62+92\(\ne\)112 nên không phải là tam giác vuông
Trắc nhiệm2
Cho tam giác ABC và tam giác A' B' C' đối xứng với nhua qua điểm I biết AB = 4cm, AC = 8cm và chu vi của tam giác ABC = 22cm. Hỏi độ dài cạnh B' C' của tam giác A'B'C' là:
A. 9cm
B. 8cm
C. 4cm
D. 10cm
+ Ko có Trên mạng
cho tam giác ABC vuông tại A ,O là trung điểm của BC .Gọi D là điểm đối xứng của A qua O
a, chứng minh tứ giác ABCD là hình chữ nhật
b, tính chu vi hình chữ nhật trên nếu BC=10cm ,AB=8cm
a) Xét tứ giác ACDB có: O là trung điểm của BC; D là điểm đối xứng của A qua O (gt)
=> Tứ giác ACDB là hình bình hành ( 2 đường chéo cắt nhau tại trung điểm mỗi đường ) (1)
Tam giác ABC vuông tại A => AB vuông góc AC (2)
Từ (1) và (2) => ABCD là hình chữ nhật
b) Áp dụng định lý Py-ta-go vào tam giác ABC vuông tại A, ta có:
\(AB^2+AC^2=BC^2\)
=> \(AC^2=BC^2-AB^2\)
=> \(AC^2=10^2-8^2\)
=> \(AC^2=36\)
=> AC = 6 (cm)
Chu vi hình chữ nhật là \(2\left(AB+AC\right)=2\left(6+8\right)=28\left(cm\right)\)
Chúc bạn học tốt!!!
a) Xét tứ giác ABDC có
O là trung điểm của đường chéo BC
O là trung điểm của đường chéo AD
Do đó: ABDC là hình bình hành
mà \(\widehat{CAB}=90^0\)
nên ABDC là hình chữ nhật
b) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow AC^2=10^2-8^2=36\)
hay AC=6(cm)
Ta có: ABDC là hình chữ nhật(cmt)
nên \(C_{ABDC}=\left(AC+AB\right)\cdot2=\left(6+8\right)\cdot2=28\left(cm\right)\)
Cho tam giác ABC, có AB = 6cm, AC = 8cm, BC = 10cm. Q là hình chiếu của A trên cạnh BC
a. Cm tam giác ABC vuông
b. Tính BQ biết AQ = 4,8cm
c. Tia phan giác của góc B cắt AC tại D. Vẽ H là hình chiếu của D trên BC. Cm tam giác ABD = tam giác HBD
d. So sánh HQ và HC
c) Xét ΔABD vuông tại A và ΔHBD vuông tại H có
BD chung
\(\widehat{ABD}=\widehat{HBD}\)(BD là tia phân giác của \(\widehat{ABH}\))
Do đó: ΔABD=ΔHBD(cạnh huyền-góc nhọn)
a) Ta có: \(BC^2=10^2=100\)
\(AB^2+AC^2=6^2+8^2=100\)
Do đó: \(BC^2=AB^2+AC^2\)(=100)
Xét ΔABC có \(BC^2=AB^2+AC^2\)(cmt)
nên ΔABC vuông tại A(Định lí Pytago đảo)
b) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(AB^2=AQ^2+BQ^2\)
\(\Leftrightarrow BQ^2=AB^2-AQ^2=6^2-4.8^2=12.96\)
hay BQ=3,6(cm)
Vậy: BQ=3,6cm
Cho tam giác ABC vuông tại A, có AB = 6cm, AC = 8cm , BC = 10cm và tam giác DEF vuông tại D có DE = 9cm, DF = 12cm, EF = 15cm.
a) Hai tam giác ABC và DEF có đồng dạng không? Vì sao?
b) Tính tỉ số chu vi của hai tam giác ấy?
a: Xét ΔABC vuông tại A và ΔDEF vuông tại D có
AB/DE=AC/DF
Do đó: ΔABC\(\sim\)ΔDEF
b: \(\dfrac{C_{ABC}}{C_{DEF}}=\dfrac{AB}{DE}=\dfrac{2}{3}\)
Độ dài hai cạnh của một tam giác là 2cm và 10cm. Trong các số đo sau đây, số đo nào là độ dài cạnh thứ ba của tam giác đó?
(A) 6cm
(B) 7cm;
(C) 8cm ;
(D) 9cm.
Giả sử độ dài cạnh thứ ba là x ( cm ).
Theo hệ quả về bất đẳng thức tam giác ta có:
10 – 2 < x < 10 + 2
Hay 8 < x < 12
Trong các phương án chỉ có phương án D: 9cm thỏa mãn.
Chọn đáp án (D) 9cm.
Một hình tứ giác có độ dài các cạnh lần lượt là (7cm,8cm,10cm,9cm ). Chu vi của hình tứ giác đó là:
A. 15 cm
B. 25 cm
C. 24 cm
D. 34 cm
Chu vi của hình tứ giác đó là:
7 + 8 + 10 + 9 = 34 (cm )
Đáp số: 34 cm
Đáp án cần chọn là D