tính a,b,c
ac,b x ba,c x cb,a = abc,cba
thay các chữ thành các chữ số thích hợp:
a,cba+ab+cb=899
b,abc+bac+cba=1323
a)abc+ab+ca+928
b)cba+ab+cb=899
c)abc+bac+cba=1323
d)abc+acb=bea
e)a+ab+abc=bcb
g)abcd+abc+ab+a=4321
cách giải đầy đủ nha
1)
a) tim tat ca cac chu so a,b,c thoa man : abc - cba = 6b3
b) tim x biet : 1/21 + 1/28 +1/36 + ........ + 2/x(x+1) = 2/9
abc-cba=a.100+b.10+c-c.100-b.10-a
=99(a-c)=6b3
=> 6b3 chia hết cho 99=>b=9
=> a-c=693:99=7=>(a,c) E {(8;1);(9;2)}
Vậy (a,b,c) E {(8;9;1);(9;9;2)}
\(abc-cba=6b3\)
\(\Leftrightarrow100a+10b+c-100c-10b-a=600+10b+3\)
\(\Leftrightarrow99a-99c=603+10b\)
\(\Leftrightarrow99\left(a-c\right)=603+10b\)
\(\Leftrightarrow\hept{\begin{cases}a=8\\b=9\\c=1\end{cases}}\)
2/\(\frac{1}{21}+\frac{1}{28}+\frac{1}{36}+...+\frac{2}{x\left(x+1\right)}=\frac{2}{9}\)
\(\Leftrightarrow\frac{2}{42}+\frac{2}{56}+\frac{2}{72}+...+\frac{2}{x\left(x+1\right)}=\frac{2}{9}\)
\(\Leftrightarrow2\left(\frac{1}{6.7}+\frac{1}{7.8}+\frac{1}{8.9}+...+\frac{1}{x\left(x+1\right)}\right)=\frac{2}{9}\)
\(\Leftrightarrow\frac{1}{6}-\frac{1}{7}+\frac{1}{7}-\frac{1}{8}+...+\frac{1}{x}-\frac{1}{x+1}=\frac{1}{9}\)
\(\Leftrightarrow\frac{1}{6}-\frac{1}{x+1}=\frac{1}{9}\Leftrightarrow\frac{1}{x+1}=\frac{1}{6}-\frac{1}{9}\)
\(\Leftrightarrow\frac{1}{x+1}=\frac{1}{18}\Leftrightarrow x+1=18\Leftrightarrow x=17\)
bài 1 : tính nhanh
136 x 68+16 x 172
bài 2
a) ab+ ba = 165
b) abc+cba là một số có 3 chữ số và a+c =9
bài 3
cho A=1999 x 2001 ; B= 2000 x 2000
không tính hãy so sánh a và b
Giả sử ∫ 1 2 1 + x 2 x 4 d x = 1 c a a - b b + c b a ; b ; c ∈ ℕ ; 1 ≤ a , b , c ≤ 9 . Tính giá trị biểu thức S = C 2 a + c b - a .
A. 165
B. 715
C. 5456
D. 35
Chọn D.
Phương pháp: Tính tích phân để suy ra a, b, c.
Cách giải: Ta có:
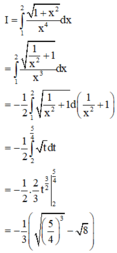
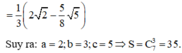
Cho △ABC vuông tại C có CB=6cm , AC=8cm. Vẽ đường cao CH của △ABC
a) Chứng minh: △HBC đồng dạng với △CBA và CH.BA=CB.AC
b) Tính độ dài các đoạn BA và CH
c) Vẽ HD ⊥ CB tại D , HE ⊥ AC tại E. tính khoảng cách từ trung điểm I của BA đến DE
Cho ABC vuông tại A. có AH là đường cao
a/ Cm ABH đồng dạng CBA suy ra AB^2=BH. CB
b/ Cho BH=4cm CB =12cm. Tính AB và AC
c/ Tính S EBH/S DBA
d/ Gọi I là hình chiếu của A trên BD M là trung điểm BE. Cm IH vuông HM
easy như 1 trò đùa dùng các tính chất của tam giác vuông ý
Cho ba số a,b,c khác 0 thoả mãn đẳng thức :a b cc =a b−cb =c b−aa Tính :P=(a b)(b c)(a c)abc
Cho ABC vuông tại A. có AH là đường cao
a/ Cm ABH đồng dạng CBA suy ra AB^2=BH. CB
b/ Cho BH=4cm CB =12cm. Tính AB và AC
c/ Tính S EBH/S DBA
d/ Gọi I là hình chiếu của A trên BD M là trung điểm BE. Cm IH vuông HM
Mình tự làm a b c được rồi bạn nào giúp mình câu d với
a) Xét \(\Delta ABH\) và \(\Delta CBA\)có:
\(\widehat{AHB}=\widehat{CAB}=90^0\)
\(\widehat{ABC}\) CHUNG
Suy ra: \(\Delta ABH~\Delta CBA\)
\(\Rightarrow\)\(\frac{AB}{CB}=\frac{BH}{AB}\)
\(\Rightarrow\)\(AB^2=BH.CB\)
b) \(\Delta ABH~\Delta CBA\)
\(\Rightarrow\)\(\frac{AB}{BC}=\frac{HB}{AB}\)
\(\Rightarrow\)\(AB^2=BC.HB=12.4=48\)
\(\Rightarrow\)\(AB=\sqrt{48}=4\sqrt{3}\)
Áp dụng định lý Pytago vào tam giác vuông ABC ta có:
\(AC^2=BC^2-AB^2\)
\(\Leftrightarrow\)\(AC^2=12^2-\left(4\sqrt{3}\right)^2=96\)
\(\Leftrightarrow\)\(AC=\sqrt{96}=4\sqrt{6}\)