Cho tam giác ABC cân tại A có : AH ⊥ BC tại H. Tính số đo góc BAH biết B A C ^ = 50 °
A. 30 °
B. 25 °
C. 20 °
D. 35 °
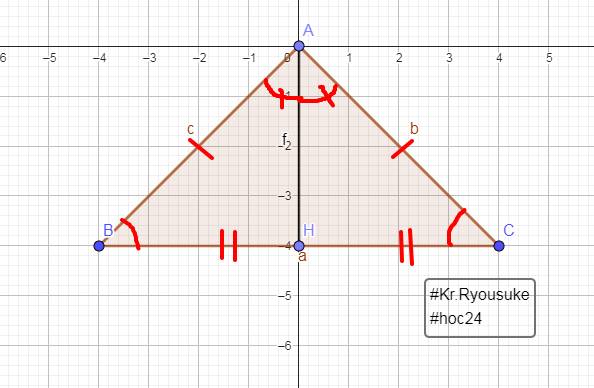
cho tam giác ABC cân tại A, đường cao AH (H thuộc BC)
a. tam giác AHB có bằng tam giác AHC không?vì sao?
b. cho góc BAH có số đo bằng 35 độ. tính số đo góc CAH?
c. cho BH=4cm. tính độ dài đoạn thẳng CH?
`a,`
Vì `\Delta ABC` cân tại A:
`-> \text {AB = AC, }` $\widehat {B} = \widehat {C}$.
Xét `\Delta AHB` và `\Delta AHC` :
`\text {AB = AC}`
$\widehat {B} = \widehat {C}$
$\widehat {AHB} = \widehat {AHC} (=90^0) (\text {AH là đường cao})$
`=> \Delta AHB = \Delta AHC (ch-gn)`
`b,`
Vì `\Delta AHB = \Delta AHC (a)`
`->` $\widehat {BAH} = \widehat {CAH} (\text {2 góc tương ứng})$
Mà $\widehat {BAH} = 35^0$
`->` $\widehat {BAH} = \widehat {CAH} = 35^0.$
`c,`
`\Delta AHB = \Delta AHC (a)`
`-> \text {BH = CH (2 cạnh tương ứng)}`
Mà `\text {BH = 4 cm}`
`-> \text {BH = CH = 4 cm}`
a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
=>ΔAHB=ΔAHC
b: góc CAH=góc BAH=35 độ
c: HC=HB=4cm
Bài 1: Cho tam giác ABC cân tại A biết rằng trên cạnh BC có điểm D sao cho BD=AB tính số đo góc A
Bài 2: Cho tam giác ABC có 2 đường cao BD, CE cắt nhau tại H. Biết AB=CH, tính số đo góc ACB
Bài 3: Cho tam giác ABC có AH, AM lần lượt là đường cao, đường trung tuyến của tam giác. Biết góc BAH=góc HAM=góc MAC=góc \(\frac{\widehat{BAC}}{3}\)
Bài 4: Cho tam giác ABC cân tại A có góc A=100o . Trên tia AB lấy điểm D sao cho AD=BC. Tính góc ACD
Bài 5: Cho tam giác ABC có góc B=60o , góc C=75o . Trên tia đối tia BC lấy điểm M sao cho BC=2BM. Tính số đo các góc M
cho tam giác ABC vuông tại A. Kr AH vuông góc với BC, H thuộc BC . đường thẳng vuông góc BC vuống vs đg thẳng AH cắt tại K.
a) tính tam giác ABE và tam giác BAH
B) CHO C bắng 30 độ. tính số đo
c) tính số đo góc BKc
Bạn ghi lại đề nhé. Tính tam giác có nghĩa là gì ? điểm K chưa xác định rõ.
Cho tam giác ABC vuông tại A có 11góc B= 7 góc C
a, tính số đo các góc của tam giác ABC
b, kẻ AH vuông góc với BC ( H thuộc BC ). Tính góc BAH và góc CAH
1.Cho tam giác ABC vuông tại A. Vẽ AH vuông góc với BC tại H. Chứng minh rằng góc B= góc HAC, góc C= góc BAH
2. Cho tam giác ABC có góc A=a. Hai tia phân giác của hai góc B,C cắt nhau tại I. Tính số đo góc BIC theo a.
Xét tam giác ABC có:
^A+^B+^C=180°(đl tổng ba góc tam giác)
=>^B+^C=180°-a
Vì BI là pg ^B
=>^ABI=^IBC=1/2^B
Vì CI là pg ^C
=>^BCI=^ICA=1/2^C
Ta có:^B+^C=180°-a
=>(^B+^C)/2=(180°-a)/2
=>^IBC+^BCI=90°-a/2
Xét tam giác BIC có:
^IBC+^BCI+^BIC=180°(đl tổng ba góc tam giác)
=>^BIC=180°-90°-a/2
=>^BIC=90°+a/2
Bạn vẽ hình giúp mình nhé. Mình chỉ giải thôi nha!
1.Vì AH vuông góc với BC
=>^AHC=90°
Xét tam giác HAC vuông tại H
=>^HAC+^C=90°
=>^HAC=90° -^C (1)
Xét tam giác ABC vuông tại A
=>^B+^C=90°
=>^B=90° - ^C (2)
Từ (1) và (2)=>đpcm
-----------------------------------------------------------------
Câu này cm tương tự
Để tối tớ lm câu hai nha bạn. H tớ phải đi học r ạ
cho tam giác ABC cân tại A , B=30 độ kẻ AH vuông góc với BC ( H thuộc BC ) a tính số đo góc A b chứng minh góc BAH = góc CAH c cho AH = 3cm , HC = 4cm tính độ dài AC d kẻ HE vuông góc với AB , HF vuông goc với AC ( E thuộc AB , F thuộc AC ) . Chứng minh HE = HF
d) Xét ΔHEB vuông tại E và ΔHFC vuông tại F có
HB=HC(ΔABH=ΔACH)
\(\widehat{B}=\widehat{C}\)(ΔABC cân tại A)
Do đó: ΔHEB=ΔHFC(Cạnh huyền-góc nhọn)
Suy ra: HE=HF(Hai cạnh tương ứng)
cho tam giác ABC cân tại A , B=30 độ kẻ AH vuông góc với BC ( H thuộc BC ) a tính số đo góc A b chứng minh góc BAH = góc CAH c cho AH = 3cm , HC = 4cm tính độ dài AC d kẻ HE vuông góc với AB , HF vuông goc với AC ( E thuộc AB , F thuộc AC ) . Chứng minh HE = HF
a. Ta có : \(\widehat{B}\)=30 MÀ ΔABC CÂN TẠI A
⇒\(\widehat{C}\)=30
MÀ \(\widehat{A}+\widehat{B}+\widehat{C}\)=180
⇒\(\widehat{A}\) + 30+30=180
⇒\(\widehat{A}\)=180-30-30
⇒\(\widehat{A}\)=120
xÉT ΔAHB vuông tại H, ΔAHC vuông tại H
CÓ : AB = AC (TAM GIÁC ABC CÂN TẠI A)
\(\widehat{B}=\widehat{C}\)(TAM GIÁC ABC CÂN TẠI A)
⇒ΔAHB = ΔAHC (C.HUYỀN-G.NHỌN)
⇒\(\widehat{BAH}=\widehat{CAH}\)
C.TRONG TAM GIÁC AHC VUÔNG TẠI H
⇒\(AC^2=HC^2+AH^2\)
⇒\(AC^2\)=\(4^2\)+\(3^2\)
⇒\(AC^2\)=16+9
AC=\(\sqrt{25}\)=5CM
D.XÉT ΔAHE VUÔNG TẠI E, ΔAHF VUÔNG TẠI F
CÓ: AH : CẠNH HUYỀN CHUNG
\(\widehat{BAH}=\widehat{CAH}\) (ΔAHB = ΔAHC)
⇒ΔAHE=ΔAHF( C.HUYỀN-G.NHỌN)
⇒HE=HF (2 CẠNH TƯƠNG ỨNG)
b) Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC(ΔABC cân tại A)
AH chung
Do đó: ΔABH=ΔACH(cạnh huyền-cạnh góc vuông)
Suy ra: \(\widehat{BAH}=\widehat{CAH}\)(hai góc tương ứng)
Cho tam giác ABC cân tại A, kẻ AH vuông góc BC ( H thuộc BC) a. Chứng minh : BH = HC và góc BAH = góc CAH b. Biết AB = AC = 5cm; BC = 8cm. Tính AH
a) Xét tam giác ABH và tam giác ACH có:
\(\widehat{AHB}=\widehat{AHC}=90^0\) (gt)
\(AB=AC\) (Do tam giác ABC cân tại A)
\(AH\) chung
\(\Rightarrow\Delta ABH=\Delta ACH\) (ch-cgv) \(\Rightarrow BH=CH\) (2 cạnh tương ứng)
b) Do \(\Delta ABH=\Delta ACH\Rightarrow\widehat{BAH}=\widehat{CAH}\) (2 góc tương ứng)
c) Do \(BH=CH\Rightarrow BH=CH=\dfrac{1}{2}BC=4\left(cm\right)\)
Áp dụng ĐL Pytago ta có: \(AB^2=AH^2+BH^2\)
\(5^2=AH^2+4^2\Rightarrow AH^2=5^2-4^2=9\Rightarrow AH=3\left(cm\right)\)
Cho tam giác ABC cân tại A . Đường cao BD và CE cắt nhau tại H b) Chứng minh AH vuông góc BC c) Biết , Biết AB=70° Tính số đo của góc BHC