Tỉ số SABC:SABM biết M thuộc cạnh BC của tam giác ABC và MC=2MC

Những câu hỏi liên quan
Bài 9 (1 điểm) Cho tam giác ABC có M là điểm thuộc cạnh BC sao cho BC 3 x MC và N là điểm thuộc cạnh AC sao cho AC 4 x AN. Kéo dài MN cắt AB kéo dài tại P. Tính tỉ số diện tích tam giác PAN và tam giác ABC.Bài 10 (1 điểm) Cho tam giác ABC có M là trung điểm AB. N là điểm thuộc cạnh AC sao cho AC 3 x NC. Gọi P là trung điểm AN, Q là trung điểm MN. Tính diện tích tam giác PQN biết diện tích tam giác ABC là 180cm2.1 điểm
Đọc tiếp
Bài 9 (1 điểm) Cho tam giác ABC có M là điểm thuộc cạnh BC sao cho BC = 3 x MC và N là điểm thuộc cạnh AC sao cho AC = 4 x AN. Kéo dài MN cắt AB kéo dài tại P. Tính tỉ số diện tích tam giác PAN và tam giác ABC.
Bài 10 (1 điểm) Cho tam giác ABC có M là trung điểm AB. N là điểm thuộc cạnh AC sao cho AC = 3 x NC. Gọi P là trung điểm AN, Q là trung điểm MN. Tính diện tích tam giác PQN biết diện tích tam giác ABC là 180cm2.
1 điểm
giúp mik nhé, mik đang cần gấp
Tỉ số SABC :SABM biết M tuộc cạnh BC cùa tam giác ABC và MC=2MB
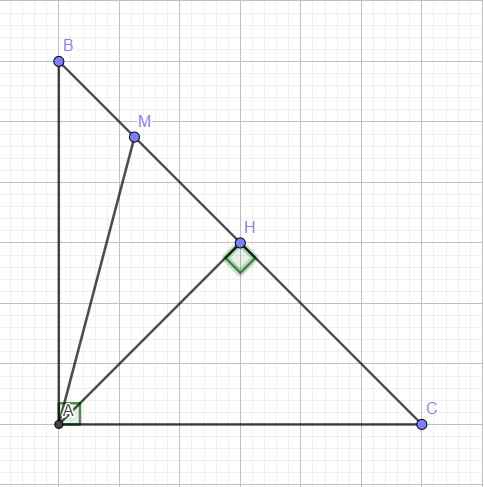
cho hình vẽ.
Ta có BM+CM=BC(vì M thuộc BC) và MC=2*BM=>3*BM=BC=>BM=1/3BC
Ta có SABC=(AH*BC)/2 hay (AH*3*BM)/2
SABM=(AH*BM)/2
=>SABC/SABM=(AH*3*BM)/2*2/(AH*BM)=(AH*3*BM)/(AH*BM)=3
Vậy SABC/SABM=3
Đúng 0
Bình luận (0)
Cho tam giác ABC, điểm M nằm trên cạnh BC sao cho BM = 2MC, điểm N trên cạnh CA sao cho CN = 3NA. Gọi D là giao điểm của AM và BN. Tính diện tích tam giác ABC nếu biết diện tích tam giác AND bằng 10cm2.
cho tam giác ABC và K là một điểm thuộc đường trung tuyến BD sao cho KB/KD=1/2. đường thẳng AK cắt cạnh BC tại điểm M. tỉ số MB/MC bằng
Cho tam giác ABC , điểm M trên cạnh BC sao cho BM = 2MC , điểm N trên cạnh CA sao cho CN = 3NA . Gọi D là giao điểm của AM và BN . Tính diện tích tam giác ABC nếu biết diện tích tam giác ADN = 10 cm2
#)Giải :
Ta có : CN = 3NA hay CA = 4NA
=> SAND = 1/4SADC (CA = 4NA, chung đường cao kẻ từ D)
=> SADC = 10 x 40 = 40 (cm2)
Lại có SAMC = 1/2SAMB (BM = 2MC, chung đường cao kẻ từ A), vì cả hai tam giác cùng có AM chung nên đường cao kẻ từ B gấp 2 lần đường cao kẻ từ C xuống AM
Và hai đường cao này là hai đường cao của hai tam giác ADB và ADC
=> SADC = 1/2SADB => SADB = 40 x 2 = 80 (cm2)
=> SANB = SAND + SADB = 10 + 80 = 90 (cm2)
Mà SANB = 1/4SABC (CA = 4NA, chung đường cao kẻ từ A)
=> SABC = 90 x 4 = 360 (cm2)
Đúng 0
Bình luận (0)
Cho tam giác ABC. Điểm M thuộc cạnh BC sao cho MB : MC = 2 : 3. Kẻ MH // AC (H thuộc AB) và MK // AB (K thuộc AC).
a) Tính MB, MC biết BC = 25cm
b) Tính chu vi tam giác ABC biết chu vi KMC bằng 30cm
c) Chứng minh rằng HB.MC = BM.KM
Cho tam giác ABC. Điểm M thuộc cạnh BC sao cho MB : MC = 2 : 3. Kẻ MH // AC (H thuộc AB) và MK // AB (K thuộc AC).
a) Tính MB, MC biết BC = 25cm
b) Tính chu vi tam giác ABC biết chu vi KMC bằng 30cm
c) Chứng minh rằng HB.MC = BM.KM
Cho tam giác ABC vuông cân tại A, đường cao AH. Trên cạnh BC lấy điểm M tùy ý. Chính minh rằng tỉ số \(\dfrac{MA^2}{MB^2+MC^2}\) không phụ thuộc vào vị trí của điểm M. Giá trị của tỉ số đó là bao nhiêu?
Do tính đối xứng, không mất tính tổng quát, giả sử M nằm giữa B và H
ABC vuông cân \(\Rightarrow BH=CH=AH\)
Ta có:
\(\dfrac{MA^2}{MB^2+MC^2}=\dfrac{MA^2}{\left(BH-MH\right)^2+\left(CH+MH\right)^2}=\dfrac{MA^2}{\left(BH-MH\right)^2+\left(BH+MH\right)^2}\)
\(=\dfrac{MA^2}{2\left(BH^2+MH^2\right)}=\dfrac{MA^2}{2\left(AH^2+MH^2\right)}=\dfrac{MA^2}{2MA^2}=\dfrac{1}{2}\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông cân tại A, đường cao AH. Trên cạnh BC lấy điểm M tùy ý. Chứng minh rằng tỉ số \(\dfrac{MA^2}{MB^2+MC^2}\) không phụ thuộc vào vị trí của điểm M. Giá trị của tỉ số đó là bao nhiêu?
Do tính đối xứng, ko mất tính tổng quát, giả sử M nằm giữa B và H
ABC vuông cân \(\Rightarrow AH\) đồng thời là trung tuyến
\(\Rightarrow AH=\dfrac{1}{2}BC\Rightarrow AH=BH=CH\)
Ta có:
\(\dfrac{MA^2}{MB^2+MC^2}=\dfrac{MA^2}{\left(BH-HM\right)^2+\left(CH+MH\right)^2}=\dfrac{MA^2}{\left(AH-MH\right)^2+\left(AH+MH\right)^2}\)
\(=\dfrac{MA^2}{2\left(AH^2+MH^2\right)}=\dfrac{MA^2}{2MA^2}=\dfrac{1}{2}\)
Đúng 0
Bình luận (0)