Question

Cho tam giác ABC vuông cân tại A, đường cao AH. Trên cạnh BC lấy điểm M tùy ý. Chứng minh rằng tỉ số \(\dfrac{MA^2}{MB^2+MC^2}\) không phụ thuộc vào vị trí của điểm M. Giá trị của tỉ số đó là bao nhiêu?

 

Answer 1

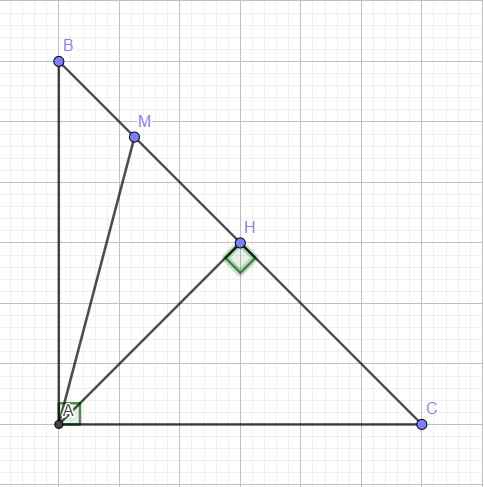
Do tính đối xứng, ko mất tính tổng quát, giả sử M nằm giữa B và H

ABC vuông cân \(\Rightarrow AH\) đồng thời là trung tuyến

\(\Rightarrow AH=\dfrac{1}{2}BC\Rightarrow AH=BH=CH\)

Ta có:

\(\dfrac{MA^2}{MB^2+MC^2}=\dfrac{MA^2}{\left(BH-HM\right)^2+\left(CH+MH\right)^2}=\dfrac{MA^2}{\left(AH-MH\right)^2+\left(AH+MH\right)^2}\)

\(=\dfrac{MA^2}{2\left(AH^2+MH^2\right)}=\dfrac{MA^2}{2MA^2}=\dfrac{1}{2}\)

Answer 2