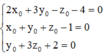Trong không gian Oxyz cho tam giác MNP với M 1 ; 0 ; 0 , N 0 ; 0 ; 1 , P 2 ; 1 ; 1 . Góc M của tam giác MNP bằng:
A. 45 °
B. 60 °
C. 90 °
D. 120 °
Trong không gian với hệ tọa độ Oxyz, cho ba điểm M 3 ; 2 ; 8 , N 0 ; 1 ; 3 , P 2 ; m ; 4 . Tìm m để tam giác MNP vuông tại N.
A. m = 25
B. m = 4
C. m = -1
D. m = -10
Trong không gian với hệ tọa độ Oxyz, cho ba điểm M = 3 ; 2 ; 8 , N 0 ; 1 ; 3 và P = 2 ; m ; 4 . Tìm m để tam giác MNP vuông tại N.
A. m = 25.
B. m = 4
C. m = - 1
D. m = - 10
Đáp án D.
Ta có: N M ¯ = 3 ; 1 ; 5 N P ¯ 2 ; m − 1 ; 1 do đó tam giác MNP vuông tại N khi
N M ¯ . N P ¯ = 6 + 1. m − 1 + 5 = 0
⇔ m = − 10.
Trong không gian với hệ tọa độ Oxyz, cho ba điểm M(3;2;8), N(0;1;3), P(2;m;4). Tìm m để tam giác MNP vuông tại N.
A. m = 25
B. m = 4
C. m = -1
D. m = -10
Trong không gian với hệ trục tọa độ Oxyz cho tam giác MNP biết M N ⇀ = - 3 ; 0 ; 4 và N P ⇀ = - 1 ; 0 ; - 2 . Độ dài đường trung tuyến MI của tam giác MNP bằng:
A. 9 2
B.
85
2
C. 95 2
D. 15 2
Trong không gian với hệ tọa độ Oxyz, cho ba điểm M(3;2;8), N(0;1;3) và P(2;m;4). Tìm m để tam giác MNP vuông tại N.
A. m= 25
B. m= 4
C. m= -1
D. m= -10
Đáp án D.

do đó tam giác MNP vuông tại N khi
![]()
Trong không gian với hệ tọa độ Oxyz, cho ba điểm M(3;2;8), N(0;1;3) và P(2;m;4). Tìm m để tam giác MNP vuông tại N.
A. m=25
B. m=4
C. m=-1
D. m=-10
Trong không gian với hệ tọa độ Oxyz, cho ba điểm M(1;1;1);N(1;0;-2),P(0;1;-1). Gọi G ( x 0 ; y 0 ; z 0 ) là trực tâm tam giác MNP. Tính x 0 + z 0
A. 0
B. - 13 7
C. 5 2
D. -5
M(1;1;1);N(1;0;-2),P(0;1;-1) ⇒ N P ⇀ = - 1 ; 1 ; 1 ; M P ⇀ = - 1 ; 0 ; - 2
⇒ N P ⇀ ; M P ⇀ = - 2 ; - 3 ; 1
Phương trình mặt phẳng (MNP) là
![]()
![]()
G là trực tâm tam giác MNP

⇔
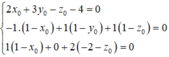
⇔
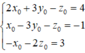
⇔
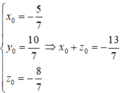
Chọn đáp án B.
Trong không gian với hệ trục tọa độ Oxyz, cho 3 điểm M(1;1;1), N(1;0;-2), P(0;1;-1). Gọi G x 0 ; y 0 ; z 0 là trực tâm tam giác MNP. Tính x 0 + z 0
A. -5
B. 5 2
C. - 13 7
D. 0
Đáp án B
Phương pháp: G là trực tâm tam giác MNP
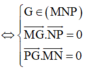
Cách giải: Gọi G x 0 ; y 0 ; z 0 là trực tâm tam giác MNP
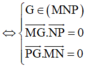
![]()
Mặt phẳng (MNP) có một VTPT
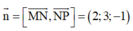
Phương trình (MNP) 2x+3y-z-4=0
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Từ (1),(2),(3), suy ra
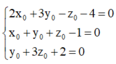
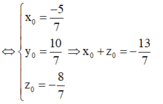
Trong không gian với hệ trục tọa độ Oxyz, cho 3 điểm M(1;1;1), N(1;0; - 2), P(0;1; - 1). Gọi G(x0;y0;z0) là trực tâm tam giác MNP. Tính x0 + z0
A. - 5
B. 5/2
C. - 13/7
D. 0
Đáp án C
Phương pháp: G là trực tâm tam giác MNP 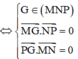
Cách giải: G(x0;y0;z0) là trực tâm tam giác MNP 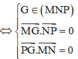
![]()
Mặt phẳng (MNP) có một VTPT ![]()
Phương trình (MNP): 2x+3y-z-4=0
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Từ (1),(2),(3), suy ra