M(1;1;1);N(1;0;-2),P(0;1;-1) ⇒ N P ⇀ = - 1 ; 1 ; 1 ; M P ⇀ = - 1 ; 0 ; - 2
⇒ N P ⇀ ; M P ⇀ = - 2 ; - 3 ; 1
Phương trình mặt phẳng (MNP) là
![]()
![]()
G là trực tâm tam giác MNP

⇔
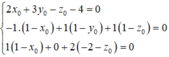
⇔
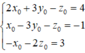
⇔
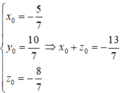
Chọn đáp án B.
M(1;1;1);N(1;0;-2),P(0;1;-1) ⇒ N P ⇀ = - 1 ; 1 ; 1 ; M P ⇀ = - 1 ; 0 ; - 2
⇒ N P ⇀ ; M P ⇀ = - 2 ; - 3 ; 1
Phương trình mặt phẳng (MNP) là
![]()
![]()
G là trực tâm tam giác MNP

⇔
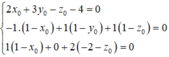
⇔
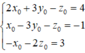
⇔
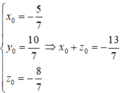
Chọn đáp án B.
Trong không gian với hệ trục tọa độ Oxyz, cho 3 điểm M(1;1;1), N(1;0; - 2), P(0;1; - 1). Gọi G(x0;y0;z0) là trực tâm tam giác MNP. Tính x0 + z0
A. - 5
B. 5/2
C. - 13/7
D. 0
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d: x - 2 1 = y - 2 2 = z + 2 - 1 và mặt phẳng ( α ) :2x+2y-z-4=0. Tam giác ABC có A(-1;2;1), các đỉnh B, C nằm trên (α) và trọng tâm G nằm trên đường thẳng d. Tọa độ trung điểm M của BC là
A. M(2;1;2)
B. M(0;1;-2)
C. M(1;-1;-4)
D. M(2;-1;-2)
Trong không gian với hệ tọa độ Oxyz, cho phương trình mặt phẳng (P): x+2y+z-8=0 và ba điểm A(0;-1;0),B(2;3;0),C(0;-5;2). Gọi M ( x 0 ; y 0 ; z 0 ) là điểm thuộc mặt phẳng (P) sao cho MA=MB=MC. Tổng S = x 0 + y 0 + z 0 bằng
A. -12
B. -5
C. 9
D. 12
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(1;1;1), B(0;1;2), C(–2;1;4) và mặt phẳng(P): x – y + z + 2 = 0. Tìm điểm N ∈ (P) sao cho S = 2 N A 2 + N B 2 + N C 2 đạt giá trị nhỏ nhất.
A. N - 2 ; 0 ; 1
B. N - 4 3 ; 2 ; 4 3
C. N - 1 2 ; 5 4 ; 3 4
D. N - 1 ; 2 ; 1
Trong không gian với hệ trục tọa độ Oxyz, cho điểm A(1;0;-1) và mặt phẳng P : x + y - z - 3 = 0 . Gọi (S) là mặt cầu có tâm I nằm trên mặt phẳng (P), đi qua điểm A và gốc tọa độ O sao cho diện tích tam giác OIA bằng 17 2 . Tính bán kính R của mặt cầu (S)
A. R = 3
B. R = 9
C. R = 1
D. R = 5
Trong không gian với hệ tọa độ Oxyz, cho điểm A (1;0;-1) và mặt phẳng P : x + y - z - 3 = 0 . Gọi (S) là mặt cầu có tâm I nằm trên mặt phẳng (P), đi qua điểm A và gốc tọa độ O sao cho diện tích tam giác OIA bằng 17 2 . Tính bán kính R của mặt cầu (S).
A. R = 3
B. R = 9
C. R = 1
D. R = 5
Trong không gian với hệ tọa độ Oxyz, cho 3 điểm A(a;0;0), B(1;b;0), C(1;0;c), với a,b,c là các số thực thay đổi sao cho H(3;2;1) là trực tâm của tam giác ABC. Tính S=a+b+c.
A. S = 2
B. S = 19
C. S = 11
D. S = 9
Trong không gian với hệ tọa độ Oxyz, cho ba mặt phẳng (α): x +y +2z +1 =0; (β): x +y –z +2 =0; (γ):x –y +5 =0. Mệnh đề nào sau đây sai?
A. α ⊥ γ
B. (α)//(γ).
C. γ ⊥ β
D. α ⊥ β
Trong không gian với hệ tọa độ Oxyz cho điểm A(2;-1;0) và mặt phẳng ( P ) : x - 2 y + z + 2 = 0 . Gọi I là hình chiếu vuông góc của A trên mặt phẳng (P). Phương trình mặt cầu đi qua A và có tâm I là
A. x + 1 2 + y + 1 2 + z + 1 2 = 6
B. x + 1 2 + y - 1 2 + z + 1 2 = 6
C. x - 1 2 + y - 1 2 + z + 1 2 = 6
D. x + 1 2 + y + 1 2 + z - 1 2 = 6