Đáp án C
Phương pháp: G là trực tâm tam giác MNP 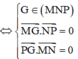
Cách giải: G(x0;y0;z0) là trực tâm tam giác MNP 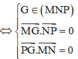
![]()
Mặt phẳng (MNP) có một VTPT ![]()
Phương trình (MNP): 2x+3y-z-4=0
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Từ (1),(2),(3), suy ra 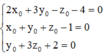

Đáp án C
Phương pháp: G là trực tâm tam giác MNP 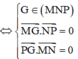
Cách giải: G(x0;y0;z0) là trực tâm tam giác MNP 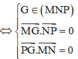
![]()
Mặt phẳng (MNP) có một VTPT ![]()
Phương trình (MNP): 2x+3y-z-4=0
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Từ (1),(2),(3), suy ra 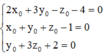

Trong không gian với hệ tọa độ Oxyz, cho ba điểm M(1;1;1);N(1;0;-2),P(0;1;-1). Gọi G ( x 0 ; y 0 ; z 0 ) là trực tâm tam giác MNP. Tính x 0 + z 0
A. 0
B. - 13 7
C. 5 2
D. -5
Trong không gian với hệ tọa độ Oxyz, cho phương trình mặt phẳng (P): x+2y+z-8=0 và ba điểm A(0;-1;0),B(2;3;0),C(0;-5;2). Gọi M ( x 0 ; y 0 ; z 0 ) là điểm thuộc mặt phẳng (P) sao cho MA=MB=MC. Tổng S = x 0 + y 0 + z 0 bằng
A. -12
B. -5
C. 9
D. 12
Trong không gian với hệ trục tọa độ Oxyz, cho tam giác ABC biết A (2;0;0), B (0;2;0), C (1;1;3). Gọi H x 0 ; y 0 ; z 0 là chân đường cao hạ từ đỉnh A xuống BC. Khi đó x 0 + y 0 + z 0 bằng bao nhiêu?
A. 38 9
B. 34 11
C. 30 11
D. 11 34
Trong không gian với hệ trục tọa độ Oxyz cho các điểm A(4;2;5) B(0;4;-3) C(2;-3;7) Biết điểm M(x0;y0;z0) nằm trên mặt phẳng Oxy sao cho M A ⇀ + M B ⇀ + M C ⇀ đạt giá trị nhỏ nhất. Tính tổng P=x0+y0+z0
A. P=-3
B. P=0
C. P=3
D. P=6
Trong không gian với hệ trục Oxyz, cho tam giác ABC có A 3 ; 3 ; 2 , B − 1 ; 2 ; 0 , C 1 ; 1 ; − 2 . Gọi G x 0 ; y 0 ; z 0 là trọng tâm của tam giác đó. Tổng x 0 + y 0 + z 0 bằng
A. 9.
B. 1 3 .
C. − 2 3 .
D. 3.
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng P : x + 2 y + z - 8 = 0 và ba điểm A 0 ; - 1 ; 0 , B 2 ; 3 ; 0 , C 0 ; - 5 ; 2 . Gọi M x 0 ; y 0 ; z 0 là điểm thuộc mặt phẳng (P) sao cho MA = MB = MC. Tổng S = x 0 + y 0 + z 0 bằng
A. -12
B. -5
C. 12
D. 9
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(2;-3;7), B(0;4;-3), C(4;2;5). Biết điểm M( x 0 ; y 0 ; z 0 ) nằm trên mặt phẳng (Oxy) sao cho M A → + M B → + M C → có giá trị nhỏ nhất. Khi đó giá trị của tổng P = x 0 + y 0 + z 0 bằng
A. P = 0
B. P = 6
C. P = 3
D. P = -3
Trong không gian với hệ trục tọa độ Oxyz, cho các điểm A(1;2;3) và B(3;4;1). Đặt
P = M A → + M B → trong đó M x 0 ; y 0 ; z 0 là một điểm nằm trên (Oxy) thỏa mãn P m i n . Khi đó, x 0 + y 0 + z 0 =
A. 4
B. 7 2
C. 6
D. 1
Trong không gian với hệ tọa độ Oxyz, cho vecto a → 1 ; - 2 ; 4 và b → x 0 ; y 0 ; z 0 cùng phương với vectơ a → . Biết vectơ b → tạo với tia Oy một góc nhọn và b → = 21 . Tính tổng x 0 + y 0 + z 0
A. x 0 + y 0 + z 0 = 3
B. x 0 + y 0 + z 0 = -3
C. x 0 + y 0 + z 0 = 6
D. x 0 + y 0 + z 0 = -6