Cho hình hộp chữ nhật A B C D . A ' B ' C ' D ' . Chứng minh rằng:
a ) B D / / B ’ D ’
b ) B B ’ / / m p ( C C ’ D ’ D ) , B ’ D ’ / / m p ( A B C D )
c ) m p ( A B B ’ A ’ ) / / m p ( D C C ’ D ’ )
Cho hình hộp chữ nhật ABCD.A'B'C'D'.
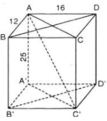
a,Chứng minh rằng tứ giác ADC'B' là hình chữ nhật.
b,Tính diện tích của hình chữ nhật ADC'B' biết: AB=12, AC'=29, DD'=16.
a: AD vuông góc DC
AD vuông góc D'D
=>AD vuông góc (DCC'D')
=>AD vuông góc DC'
Xét tứ giác ADC'B' có
AD//C'B'
AD=C'B'
góc ADC'=90 độ
=>ADC'B' là hình chữ nhật
b: AA'=16cm
AB=12cm
=>A'B=20cm
=>AB'=20cm
A'C'=căn 29^2-16^2=3*căn 65(cm)
A'B'=12cm
=>B'C'=căn A'C'^2-A'B'^2=21(cm)
S ADC'B'=21*20=420cm2
Cho hình hộp chữ nhật A B C D . A ' B ' C ' D ' . Chứng minh rằng :
a) BDD’B’ là hình chữ nhật
b ) B B ’ ⊥ m p ( A B C D ) c ) m p ( A B B ’ A ’ ) ⊥ m p ( A B C D )

a) BB’ ⊥ A’B’ (ABB’A’ là hình chữ nhật)
BB’ ⊥ B’C’ (BCC’B’ là hình chữ nhật)
=> BB’ ⊥ mp(A’B’C’D’)
=> BB’ ⊥ B’D’ hay
Hình bình hành BDD’B’ có một góc vuông nên là hình chữ nhật
BB’ vuông góc với hai đường thẳng cắt nhau AB và BC
=> BB’ ⊥ mp(ABCD)
c) mp(ABB’A’) chứa BB’ mà BB’⊥ mp(ABCD)
=> mp(ABB’A’) ⊥ mp(ABCD)
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = 12cm, AD = 16cm, AA' = 25cm.
a) Chứng minh rằng các tứ giác ACCA', BDD'B' là những hình chữ nhật.
b) Chứng minh rằng AC'2 = AB2 + AD2 + AA'2.
c) Tính diện tích toàn phần và thể tích của hình hộp chữ nhật.
a) ABCD.A’B’C’D’ là hình hộp chữ nhật
⇒ AA’ // CC’, AA’ = CC’
⇒ AA’C’C là hình bình hành
Lại có : AA’ ⊥ (ABCD) ⇒ AA’ ⊥ AC ⇒ 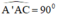
⇒ Hình bình hành AA’C’C là hình chữ nhật.
Chứng minh tương tự được tứ giác BDD'B' là những hình chữ nhật
b) Áp dụng định lý Pytago:
Trong tam giác vuông ACC’ ta có:
AC’2 = AC2 + CC’2 = AC2 + AA’2
Trong tam giác vuông ABC ta có:
AC2 = AB2 + BC2 = AB2 + AD2
Do đó: AC’2 =AB2 + AD2 + AA’2.
c) Hình hộp chữ nhật được xem như hình lăng trụ đứng.
Diện tích xung quanh:
Sxq = 2.(AB + AD).AA’
= 2.(12 + 16).25
= 1400 (cm2 )
Diện tích một đáy:
Sđ = AB.AD
= 12.16
= 192 (cm2 )
Diện tích toàn phần:
Stp = Sxq + 2Sđ
= 1400 + 2.192
= 1784 (cm2 )
Thể tích:
V = AB.AD.AA’
= 12.16.25
= 4800 (cm3 )
Cho hình hộp chữ nhật ABCD. A'B'C'D'.
a) Chứng minh rằng (BDD′B′) \( \bot \) (ABCD).
b) Xác định hình chiếu của AC′ trên mặt phẳng (ABCD).
c) Cho AB = a, BC = b, CC′ = c. Tính AC′.
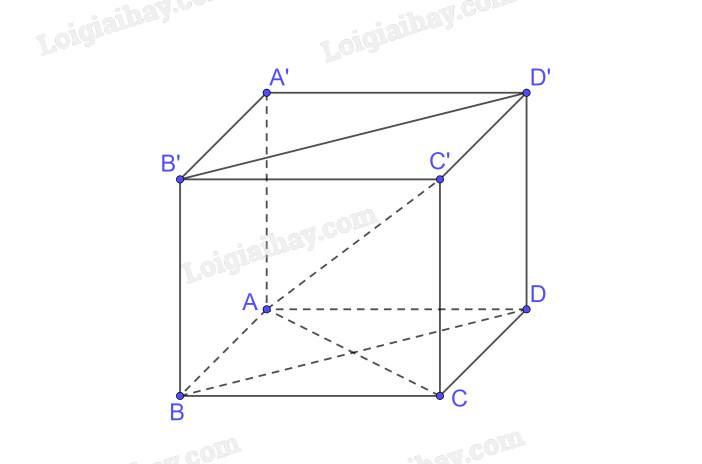
a) Ta có \(BB' \bot \left( {ABCD} \right);BB' \subset \left( {BDD'B'} \right) \Rightarrow \left( {BDD'B'} \right) \bot \left( {ABCD} \right)\)
b) A là hình chiếu của A trên (ABCD)
C là hình chiếu của C’ trên (ABCD) do \(CC' \bot \left( {ABCD} \right)\)
\( \Rightarrow \) AC là hình chiếu của AC’ trên (ABCD)
c) Xét tam giác ABC vuông tại B có
\(A{C^2} = A{B^2} + B{C^2} = {a^2} + {b^2} \Rightarrow AC = \sqrt {{a^2} + {b^2}} \)
Xét tam giác AC’C vuông tại C có
\(A{C'^2} = C{C'^2} + A{C^2} = {c^2} + {a^2} + {b^2} \Rightarrow A'C = \sqrt {{a^2} + {b^2} + {c^2}} \)
Cho hình hộp chữ nhật A,B,C,D,A’,B’,C’,D’
a) AB=5cm ,AD=7cm ,AA’=3cm .Hãy tính diện tích xung quanh,thể tích của hình hộp chữ nhật
Diện tích xung quanh:
2 x 3 x (5+7)= 72(cm2)
Thể tích của HHCN:
3 x 5 x 7 = 105(cm3)
Cho hình hộp chữ nhật A,B,C,D,A’,B’,C’,D’ a) AB=5cm ,AD=7cm ,AA’=3cm .Hãy tính diện tích xung quanh,thể tích của hình hộp chữ nhật
Sxq=(5+7)*2*3=6*12=72cm2
V=5*7*3=105cm3
Cho hình hộp chữ nhật A B C D . A ' B ' C ' D ' . Chứng minh rằng:
a ) B D / / B ’ D ’
b ) B B ’ / / m p ( C C ’ D ’ D ) , B ’ D ’ / / m p ( A B C D )
c ) m p ( A B B ’ A ’ ) / / m p ( D C C ’ D ’ )
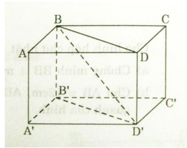
a) Ta có ABB’A’ là hình chữ nhật nên: AA’ // BB’ và AA’ = BB’
Tương tự ADD’A’ là hình chữ nhật:
AA’ // DD’ và AA’ = DD’
=> BB’ // DD’ và BB’ = DD’
Do đó BB’D’D là hình bình hành
=>BD // B’D’
b) BB’C’C là hình chữ nhật: BB’ // CC’ mà BB’ không thuộc mp(CC’D’D) và CC’ thuộc mp(CC’D’D) nên BB’ // mp(CC’D’D)
B’D’ // BD (cmt) mà B’D’ không thuộc mp (ABCD) và BD thuộc mp(ABCD) nên B’D’ // mp(ABCD)
c) Ta có: AB // CD (ABCD là hình chữ nhật)
AA’ // DD’ (ADD’A’ là hình chữ nhật)
Mà mp(ABB’A’) chứa hai đường thẳng cắt nhau AB và AA’ và mp(DCC’D’) chứa hai đường thẳng cắt nhau CD và DD’ => mp(ABB’A’) // mp(DCC’D’)
Cho hình hộp chữ nhật ABCD.A'B'C'D' như hình vẽ. Cắt
D
hình hộp theo mặt cắt MNPQ với M là trung điểm của AB và
(MNPQ) song song (AA'D'D).
a) Chứng minh NQ // (BCC'B').
b) Nếu vị trí tương đối của các cặp đường thẳng AN và BD; PB' và MN.
c) Cho AA' = 50 cm và ND' = DM = 50/2 cm. Khi đó AMND.A'QPD' là hình gì?
Cho hình hộp chữ nhật ABCD.A'B'C'D'. Có AB = a, BC= b, CC'= c.
a) Chứng minh rằng mặt phẳng (ADC'B') vuông góc với mặt phẳng (ABB'A').
b) Tính độ dài đường chéo AC' theo a, b và c.