Question

Cho hình hộp chữ nhật ABCD. A'B'C'D'.

a) Chứng minh rằng (BDD′B′) \( \bot \) (ABCD).

b) Xác định hình chiếu của AC′ trên mặt phẳng (ABCD).

c) Cho AB = a, BC = b, CC′ = c. Tính AC′.

Answer 1

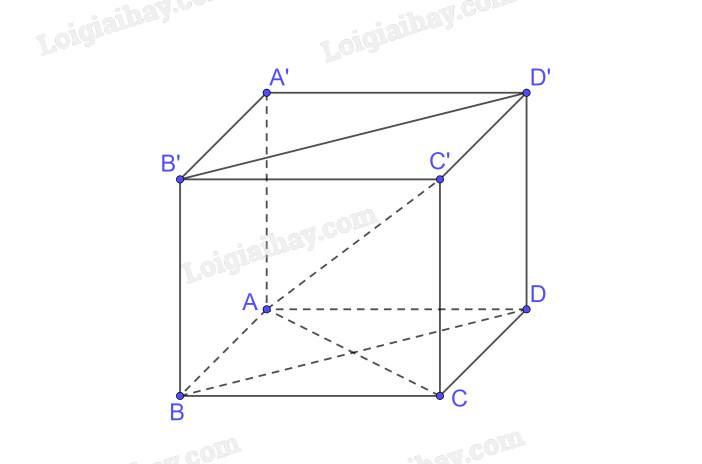
a) Ta có \(BB' \bot \left( {ABCD} \right);BB' \subset \left( {BDD'B'} \right) \Rightarrow \left( {BDD'B'} \right) \bot \left( {ABCD} \right)\)

b) A là hình chiếu của A trên (ABCD)

C là hình chiếu của C’ trên (ABCD) do \(CC' \bot \left( {ABCD} \right)\)

\( \Rightarrow \) AC là hình chiếu của AC’ trên (ABCD)

c) Xét tam giác ABC vuông tại B có

\(A{C^2} = A{B^2} + B{C^2} = {a^2} + {b^2} \Rightarrow AC = \sqrt {{a^2} + {b^2}} \)

Xét tam giác AC’C vuông tại C có

\(A{C'^2} = C{C'^2} + A{C^2} = {c^2} + {a^2} + {b^2} \Rightarrow A'C = \sqrt {{a^2} + {b^2} + {c^2}} \)