Cho hai mặt phẳng (P) và (Q). Lấy hai đường thẳng a, a' cùng vuông góc với (P), hai đường thẳng b, b' cùng vuông góc với (Q). Tìm mối quan hệ giữa các góc (a,b) và (a', b').
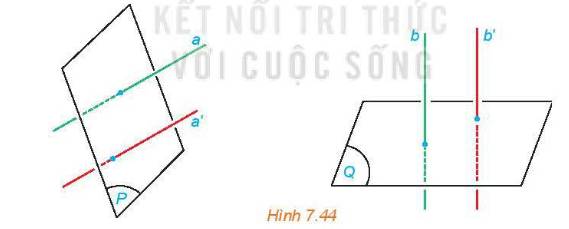
Cho hai mặt phẳng (P) và (Q). Lấy hai đường thẳng a, a' cùng vuông góc với (P), hai đường thẳng b, b' cùng vuông góc với (Q). Tìm mối quan hệ giữa các góc (a,b) và (a', b').

Góc giữa hai mặt phẳng bằng 00 khi nào, khác 00 khi nào?
Thảo luận (1)Hướng dẫn giảiGóc giữa hai mặt phẳng
+) bằng 00 khi trùng nhau
+) khác 00 khi giao nhau
(Trả lời bởi Quoc Tran Anh Le)
Cho hình chóp S.ABCD, đáy ABCD là một hình chữ nhật có tâm O, SO \( \bot \) (ABCD). Chứng minh rằng hai mặt phẳng (SAC) và (SBD) vuông góc với nhau khi và chỉ khi ABCD là một hình vuông.
Thảo luận (1)Hướng dẫn giải
\(\left. \begin{array}{l}\left( {SAC} \right) \cap \left( {SBD} \right) = SO\\\left( {SAC} \right):AC \bot SO = \left\{ O \right\}\\\left( {SBD} \right):BD \bot SO = \left\{ O \right\}\end{array} \right\} \Rightarrow \left( {\left( {SAC} \right),\left( {SBD} \right)} \right) = \left( {AC,BD} \right) = \widehat {AOB}\)
+) Nếu \(\left( {SAC} \right) \bot \left( {SBD} \right) \Rightarrow \widehat {AOB} = {90^0} \Rightarrow AC \bot BD\)
Mà ABCD là hình chữ nhật nên ABCD là hình vuông.
+) Nếu ABCD là hình vuông \( \Rightarrow AC \bot BD \Rightarrow \widehat {AOB} = {90^0}\)
\( \Rightarrow \left( {\left( {SAC} \right),\left( {SBD} \right)} \right) = {90^0} \Rightarrow \left( {SAC} \right) \bot \left( {SBD} \right)\)
(Trả lời bởi Quoc Tran Anh Le)
Cho mặt phẳng (P) chứa đường thẳng b vuông góc với mặt phẳng (Q). Lấy một đường thẳng a vuông góc với (P) (H.7.47).
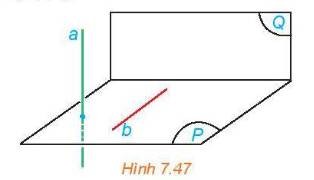
a) Tính góc giữa a và b.
b) Tính góc giữa (P) và (Q).
Thảo luận (1)Hướng dẫn giảia) \(\left. \begin{array}{l}a \bot \left( P \right)\\b \subset \left( P \right)\end{array} \right\} \Rightarrow a \bot b \Rightarrow \left( {a,b} \right) = {90^0}\)
b) Gọi \(\left( P \right) \cap \left( Q \right) = \Delta \)
\(\begin{array}{l}a \bot \Delta \left( {a \bot \left( P \right)} \right)\\b \bot \Delta \left( {b \bot \left( Q \right)} \right)\\ \Rightarrow \left( {\left( P \right),\left( Q \right)} \right) = \left( {a,b} \right) = {90^0}\end{array}\)
(Trả lời bởi Quoc Tran Anh Le)
Trong HĐ1 của Bài 23, ta đã nhận ra rằng đường thẳng nối các bản lề của cửa phòng vuông góc với sàn nhà. Hãy giải thích vì sao trong quá trình đóng – mở, cánh cửa luôn vuông góc với sàn nhà.
Thảo luận (1)Hướng dẫn giảitham khảo:
Trong một phòng, mặt sàn và các mặt tường đều vuông góc với nhau. Khi cánh cửa được đóng lại, thì mặt cửa cũng vuông góc với cả mặt sàn và mặt tường, nên đường thẳng nối bán lề của cánh cửa và cạnh của phòng sẽ là đường thẳng vuông góc với sàn nhà.
Trong quá trình đóng - mở cánh cửa, bán lề của cánh cửa vẫn cố định với mặt tường, nên đường thẳng nối bán lề của cánh cửa và cạnh của phòng vẫn là đường thẳng vuông góc với sàn nhà. Từ đó suy ra, trong quá trình đóng - mở, cánh cửa luôn vuông góc với sàn nhà.
(Trả lời bởi Bùi Nguyên Khải)
Cho hai mặt phẳng (P) và (Q) vuông góc với nhau. Kẻ đường thẳng a thuộc (P) và vuông góc với giao tuyến \(\Delta \) của (P) và (Q). Gọi O là giao điểm của a và \(\Delta \). Trong mặt phẳng (Q), gọi b là đường thẳng vuông góc với \(\Delta \) tại O.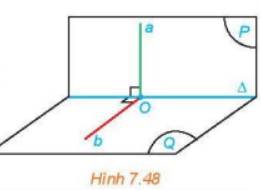
a) Tính góc giữa a và b.
b) Tìm mỗi quan hệ giữa a và (Q).
Thảo luận (1)Hướng dẫn giảia) \(\left. \begin{array}{l}\left( P \right) \cap \left( Q \right) = \Delta \\\left( P \right):a \bot \Delta \\\left( Q \right):b \bot \Delta \end{array} \right\} \Rightarrow \left( {\left( P \right),\left( Q \right)} \right) = \left( {a,b} \right)\)
Mà \(\left( P \right) \bot \left( Q \right) \Rightarrow \left( {\left( P \right),\left( Q \right)} \right) = {90^0} \Rightarrow \left( {a,b} \right) = {90^0}\)
b) \(\left( {a,b} \right) = {90^0} \Rightarrow a \bot b,a \bot \Delta ,b \cap \Delta \Rightarrow a \bot \left( Q \right)\)
(Trả lời bởi Quoc Tran Anh Le)
Cho hai mặt phẳng (P) và (Q) cắt nhau theo giao tuyến a và cùng vuông góc với mặt phẳng (R). Gọi O là một điểm thuộc a và a' là đường thẳng qua O và vuông góc với (R).
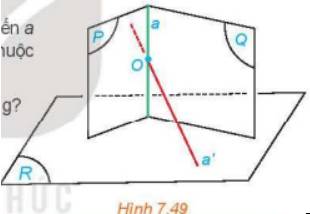
a) Hỏi a' có nằm trong các mặt phẳng (P), (Q) hay không?
b) Tìm mối quan hệ giữa a và a'.
c) Tìm mối quan hệ giữa a và (R).
Thảo luận (1)Hướng dẫn giảia) Vì O là một điểm thuộc a là giao tuyến của hai mặt phẳng (P), (Q) và a' là đường thẳng qua O và vuông góc với (R).
Theo nhận xét trang 46 thì a' có nằm trong các mặt phẳng (P), (Q).
b) Vì a' có nằm trong các mặt phẳng (P), (Q) nên a’ là giao tuyến của hai mặt phẳng (P), (Q) do đó a trùng a' (do a cũng là giao tuyến của hai mặt phẳng (P), (Q)).
c) a vuông góc với (R) do a trùng a’ và a’ vuông góc với (R).
(Trả lời bởi Quoc Tran Anh Le)
Với giả thiết như ở Ví dụ 3, chứng minh rằng:
a) Các mặt phẳng (AB'C'D') và (ABCD) cùng vuông góc với (SAC);
b) Giao tuyển của hai mặt phẳng (AB'C'D') và (ABCD) là đường thẳng đi qua A, nằm trong mặt phẳng (ABCD) và vuông góc với AC.
Thảo luận (1)Hướng dẫn giải
a) Từ ví dụ 3b ta có AB’, AC’ cùng đi qua A và vuông góc với SC
\( \Rightarrow SC \bot \left( {AB'C'D'} \right),SC \subset \left( {SAC} \right) \Rightarrow \left( {AB'C'D'} \right) \bot \left( {SAC} \right)\)
Ta có \(SA \bot \left( {ABCD} \right),SA \subset \left( {SAC} \right) \Rightarrow \left( {ABCD} \right) \bot \left( {SAC} \right)\)
Do đó các mặt phẳng (AB'C'D') và (ABCD) cùng vuông góc với (SAC).
b) Vì (AB'C'D') và (ABCD) cùng vuông góc với (SAC) nên giao tuyến của hai mặt phẳng (AB'C'D') và (ABCD) vuông góc với (SAC)
Vậy giao tuyển của hai mặt phẳng (AB'C'D') và (ABCD) là đường thẳng đi qua A, nằm trong mặt phẳng (ABCD) và vuông góc với AC.
(Trả lời bởi Quoc Tran Anh Le)
Một tài liệu hướng dẫn rằng đối với ghế bàn ăn, nên thiết kế lưng ghế tạo với mặt ghế một góc có số đo từ 100° đến 105°. Trong Hình 7.51, các tia Ox, Oy được vẽ tương ứng trên mặt ghế, lưng ghế đồng thời vuông góc với giao tuyến a của mặt ghế và lưng ghế.

a) Theo tài liệu nói trên, góc nào trong hình nên có số đo từ 100° đến 105°?
b) Nếu thiết kế theo hướng dẫn đó thì góc giữa mặt phẳng chứa mặt ghế và mặt phẳng chứa lưng ghế có thể nhận số đo từ bao nhiêu đến bao nhiêu độ?
Thảo luận (1)Hướng dẫn giảia) Theo tài liệu nói trên, góc xOy trong hình nên có số đo từ 100° đến 105°
b) Vì các tia Ox, Oy được vẽ tương ứng trên mặt ghế, lưng ghế đồng thời vuông góc với giao tuyến a của mặt ghế và lưng ghế nên góc giữa lưng ghế và mặt ghế là góc giữa Ox và Oy mà góc xOy có số đo từ 100° đến 105°
Do đó nếu thiết kế theo hướng dẫn đó thì góc giữa mặt phẳng chứa mặt ghế và mặt phẳng chứa lưng ghế có thể nhận số đo 750 đến 800
(Trả lời bởi Quoc Tran Anh Le)
Cho hình chóp S.ABC có SA \( \bot \) (ABC), AB = AC = a, \(\widehat {BAC} = {120^0},SA = \frac{a}{{2\sqrt 3 }}.\) Gọi M là trung điểm của BC.
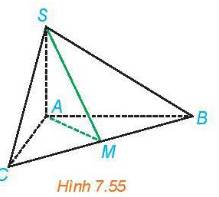
a) Chứng minh rằng \(\widehat {SMA}\) là một góc phẳng của góc nhị diện \(S, BC, A].
b) Tính số đo của góc nhị diện \(S, BC, A].
Thảo luận (1)Hướng dẫn giảia) Xét tam giác ABC có AB = AC => tam giác ABC cân tại A mà M là trung điểm BC
=> \(AM \bot BC\) (1)
\(\begin{array}{l}SA \bot BC\left( {SA \bot \left( {ABCD} \right)} \right)\\ \Rightarrow BC \bot \left( {SAM} \right);SM \subset \left( {SAM} \right) \Rightarrow BC \bot SM\,\,\,\left( 2 \right)\end{array}\)
Từ (1), (2) ta có \(\widehat {SMA}\) là một góc phẳng của góc nhị diện [S, BC, A].
b) Xét tam giác ABC cân tại A có
\(\widehat {BAC} = {120^0} \Rightarrow \widehat {ACB} = {30^0}\)
\(\sin \widehat {ACB} = \frac{{AM}}{{AC}} \Leftrightarrow \tan {30^0} = \frac{{AM}}{a} \Leftrightarrow AM = \frac{a}{{\sqrt 3 }}\)
\(\tan \widehat {SMA} = \frac{{SA}}{{AM}} = \frac{a}{{2\sqrt 3 }}:\frac{a}{{\sqrt 3 }} = \frac{1}{2} \Rightarrow \widehat {SMA} = \arctan \frac{1}{2}\)
(Trả lời bởi Quoc Tran Anh Le)