giải pt
x3-15x2+78x-141=5∛2x-9
Phân tích đa thức thành nhân tử:
+)5x2y2+15x2+30xy2
+)(x-2)(x-3)+4-x2
+)x2-7x+12
+)x3-2x2y+xy2-9x
+)x2-25+y2+2xy
+)x2-x-12
+)5x25xy-x-y
+)12y(2x-5)+6xy(5-2x)
+)16x2+24x-8xy-6y+y2
+)(x+3)(x+6)(x+9)(x+12)+81
a: \(=5x\left(xy^2+3x+6y^2\right)\)
b: \(=\left(x-2\right)\left(x+3\right)-\left(x-2\right)\left(x+2\right)=\left(x-2\right)\left(x+3-x-2\right)=\left(x-2\right)\)
c: \(=\left(x-3\right)\left(x-4\right)\)
d: \(=x\left(x^2-2xy+y^2-9\right)\)
=x(x-y-3)(x-y+3)
e: \(=\left(x+y\right)^2-25=\left(x+y+5\right)\left(x+y-5\right)\)
f: \(=\left(x-4\right)\left(x+3\right)\)
Hệ số tự do của đa thức P ( x ) = ( 15 x 2 - 7 x - x 3 ) + ( 2 x - 12 x 2 + 7 x 3 )
A. -7
B. 1
C. 2
D. 0
Giải hệ bất phương trình sau: 6 x + 5 7 < 4 x + 7 8 x + 3 2 < 2 x + 5
ập xác định D = R.
Giải từng bất phương trình ta có:
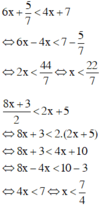
Vậy tập nghiệm của hệ bất phương trình là
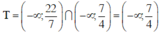
Tìm x:
1) ( 4x3 + 3x3) : x3+ ( 15x2 + 6x) : ( -3x) = 0
2) ( 25x2 - 10x) : 5x + 3 ( x - 2 ) = 4
3) ( 3x + 1 )2 - ( 2x + 1/2 ) 2 = 00
4) x2 + 8x + 16 = 0
5) 25 - 10x + x2 = 0
`1,(4x^3+3x^3):x^3+(15x^2+6x):(-3x)=0`
`<=> 4 + 3 + (-5x) + (-2)=0`
`<=> -5x+5=0`
`<=>-5x=-5`
`<=>x=1`
`2,(25x^2-10x):5x +3(x-2)=4`
`<=> 5x - 2 + 3x-6=4`
`<=> 8x -8=4`
`<=> 8x=12`
`<=>x=12/8`
`<=>x=3/2`
`3,(3x+1)^2-(2x+1/2)^2=0`
`<=> [(3x+1)-(2x+1/2)][(3x+1)+(2x+1/2)]=0`
`<=>( 3x+1-2x-1/2)(3x+1+2x+1/2)=0`
`<=>( x+1/2) (5x+3/2)=0`
`@ TH1`
`x+1/2=0`
`<=>x=0-1/2`
`<=>x=-1/2`
` @TH2`
`5x+3/2=0`
`<=> 5x=-3/2`
`<=>x=-3/2 : 5`
`<=>x=-15/2`
`4, x^2+8x+16=0`
`<=>(x+4)^2=0`
`<=>x+4=0`
`<=>x=-4`
`5, 25-10x+x^2=0`
`<=> (5-x)^2=0`
`<=>5-x=0`
`<=>x=5`
Tính phép nhân sau 1 5 x 2 + 10 x y + 20 y 2 . x 3 - 8 y 3
Giải phương trình
1) 7 - (2x + 4) = - (x +4)
2) ( x - 1) - (2x -1) = 9 - x
3) (x + 1) - (2x - 3) = ( 2x - 1)( x + 5)
\(1,\Leftrightarrow7-2x-4=-x-4\)
\(\Leftrightarrow x-2x=-4-7+4\)
\(\Leftrightarrow-x=-7\)
\(\Leftrightarrow x=7\)
Vậy \(S=\left\{7\right\}\)
\(2,\Leftrightarrow x-1-2x+1=9-x\)
\(\Leftrightarrow x+x-2x=9-1+1\)
\(\Leftrightarrow0x=9\)
\(\Rightarrow x\in\varnothing\)
Vậy \(S=\left\{\varnothing\right\}\)
\(3,\Leftrightarrow2x^2+3x-2x+3=2x^2+10x-x-5\)
\(\Leftrightarrow2x^2-2x^2+3x-2x-10x+x=-5-3\)
\(-8x=-8\)
\(\Rightarrow x=1\)
Vậy \(S=\left\{1\right\}\)
Giải pt
\(\sqrt{5-x}=9-2x\)
\(\sqrt{5-x}=9-2x\left(đk:x\le5\right)\)
\(\Leftrightarrow5-x=\left(9-2x\right)^2\)
\(\Leftrightarrow5-x=81-36x+4x^2\)
\(\Leftrightarrow4x^2-35x+76=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x_1=\dfrac{19}{4}\\x_2=4\end{matrix}\right.\) (đoạn này e tự giải đc nha)
bài 2: tìm x:
a) (4x4+3x3)÷(−x3)+(15x2+6x)÷3x=0
b)(x2−12x)÷2x−(3x−1)2÷(3x−1)=0
Bài 2: Tìm x
a)ĐKXĐ: \(x\ne0\)
Ta có: \(\left(4x^4+3x^3\right):\left(-x^3\right)+\left(15x^2+6x\right):3x=0\)
\(\Leftrightarrow\frac{-x^3\left(4x+3\right)}{x^3}+\frac{3x\left(5x+2\right)}{3x}=0\)
\(\Leftrightarrow-4x-3+5x+2=0\)
\(\Leftrightarrow x-1=0\)
hay x=1(nhận)
Vậy: x=1
b) ĐKXĐ: \(x\notin\left\{0;\frac{1}{3}\right\}\)
Ta có: \(\left(x^2-12x\right):2x-\left(3x-1\right)^2:\left(3x-1\right)=0\)
\(\Leftrightarrow\frac{x\left(x-12\right)}{2x}-\frac{\left(3x-1\right)^2}{\left(3x-1\right)}=0\)
\(\Leftrightarrow\frac{x-12}{x}-3x+1=0\)
\(\Leftrightarrow\frac{x-12}{x}=3x-1\)
\(\Leftrightarrow x-12=x\left(3x-1\right)\)
\(\Leftrightarrow3x^2-x+x-12=0\)
\(\Leftrightarrow3x^2-12=0\)
\(\Leftrightarrow3x^2=12\)
\(\Leftrightarrow x^2=4\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\left(nhận\right)\\x=-2\left(nhận\right)\end{matrix}\right.\)
Vậy: \(x\in\left\{2;-2\right\}\)
Bài 1: Giải các phương trình dưới đây
1) x2 - 9 = (x - 3)(5x +2)
2) x3 - 1 = (x - 1)(x2 - 2x +16)
3) 4x2 (x - 1) - x + 1 = 0
4) x3 + 4x2 - 9x - 36 = 0
5) (3x + 5)2 = (x - 1)2
6) 9 (2x + 1)2 = 4 (x - 5)2
7) x2 + 2x = 15
8) x4 + 5x3 + 4x2 = 0
9) (x2 - 4) - (x - 2)(3 - 2x) = 0
10) (3x + 2)(x2 - 1) = (9x2 - 4) (x + 1)
11) (3x - 1)(x2 + 2) = (3x - 1)(7x - 10)
12) (2x2 + 1) (4x - 3) = (x - 12)(2x2 + 1)
1: \(\Leftrightarrow\left(x-3\right)\left(x+3\right)-\left(x-3\right)\left(5x+2\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(-4x+1\right)=0\)
hay \(x\in\left\{3;\dfrac{1}{4}\right\}\)
2: \(\Leftrightarrow\left(x-1\right)\left(x^2+x+1\right)-\left(x-1\right)\left(x^2-2x+16\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x^2+x+1-x^2+2x-16\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(3x-15\right)=0\)
hay \(x\in\left\{1;5\right\}\)
3: \(\Leftrightarrow\left(x-1\right)\left(4x^2-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(2x-1\right)\left(2x+1\right)=0\)
hay \(x\in\left\{1;\dfrac{1}{2};-\dfrac{1}{2}\right\}\)
4: \(\Leftrightarrow x^2\left(x+4\right)-9\left(x+4\right)=0\)
\(\Leftrightarrow\left(x+4\right)\left(x-3\right)\left(x+3\right)=0\)
hay \(x\in\left\{-4;3;-3\right\}\)
5: \(\Leftrightarrow\left[{}\begin{matrix}3x+5=x-1\\3x+5=1-x\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=-6\\4x=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=-1\end{matrix}\right.\)
6: \(\Leftrightarrow\left(6x+3\right)^2-\left(2x-10\right)^2=0\)
\(\Leftrightarrow\left(6x+3-2x+10\right)\left(6x+3+2x-10\right)=0\)
\(\Leftrightarrow\left(4x+13\right)\left(8x-7\right)=0\)
hay \(x\in\left\{-\dfrac{13}{4};\dfrac{7}{8}\right\}\)
1.
\(\Leftrightarrow\left(x-3\right)\left(x+3\right)=\left(x-3\right)\left(5x-2\right)\)
\(\Leftrightarrow x+3=5x-2\)
\(\Leftrightarrow4x=5\Leftrightarrow x=\dfrac{5}{4}\)
2.
\(\Leftrightarrow\left(x-1\right)\left(x^2+x+1\right)=\left(x-1\right)\left(x^2-2x+16\right)\)
\(\Leftrightarrow x^2+x+1=x^2-2x+16\)
\(\Leftrightarrow3x=15\Leftrightarrow x=5\)
3.
\(\Leftrightarrow4x^2\left(x-1\right)-\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(4x^2-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{1}{2};x=-\dfrac{1}{2}\end{matrix}\right.\)
7.
\(\Leftrightarrow x^2+2x-15=0\)
\(\Leftrightarrow\left(x-3\right)\left(x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-5\end{matrix}\right.\)
8.\(\Leftrightarrow x^4+x^3+4x^3+4x^2=0\)
\(\Leftrightarrow x^3\left(x+1\right)+4x^2\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^3+4x^2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=0;x=-4\end{matrix}\right.\)
9.\(\Leftrightarrow\left(x-2\right)\left(x+2\right)=\left(x-2\right)\left(3-2x\right)\)
\(\Leftrightarrow x+2=3-2x\)
\(\Leftrightarrow3x=1\Leftrightarrow x=\dfrac{1}{3}\)