
Những câu hỏi liên quan
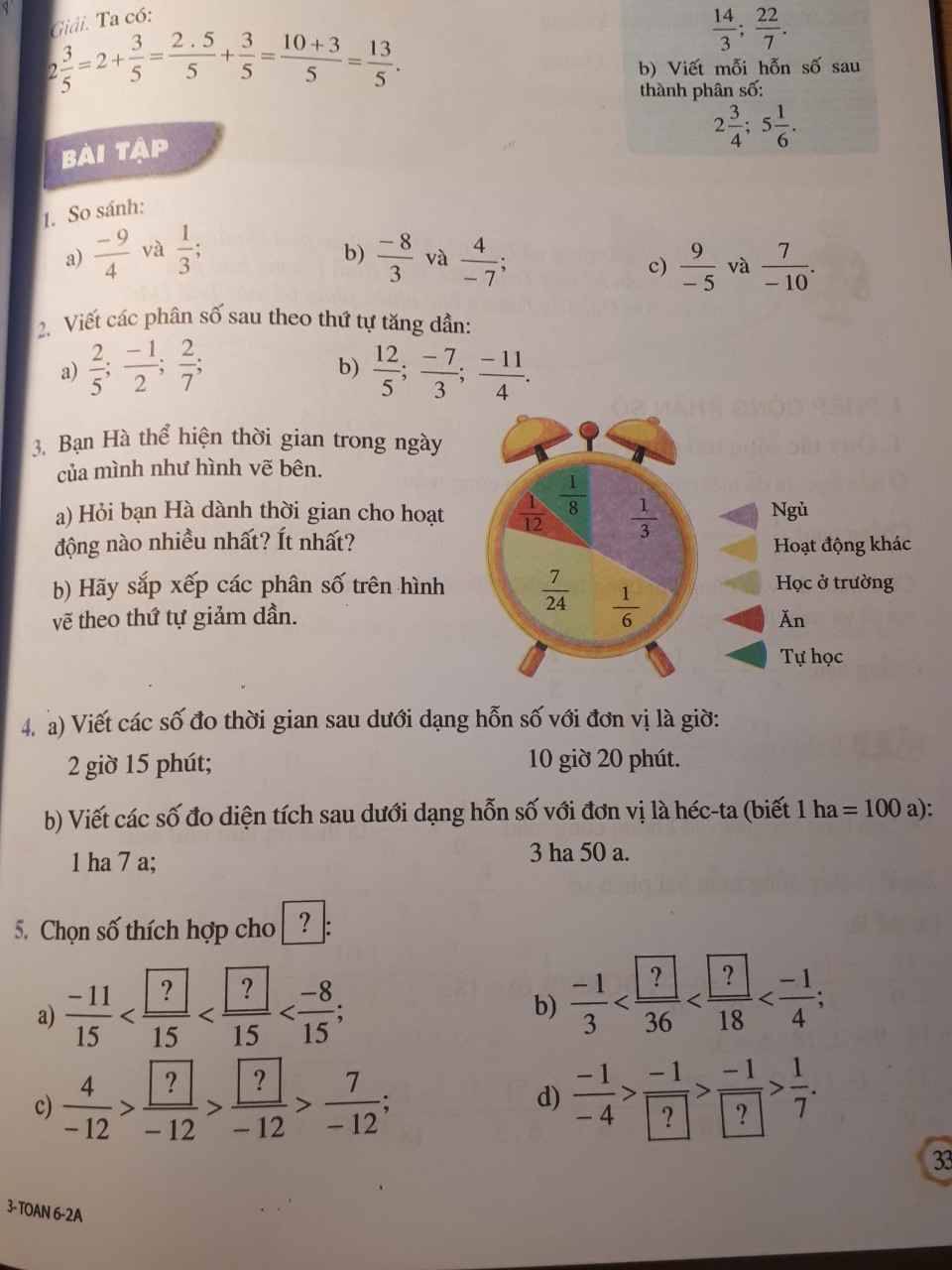 mọi người giúp mình từ câu 1 đến câu 5 với ạ
mọi người giúp mình từ câu 1 đến câu 5 với ạ
cảm ơn trước ạ
Câu 1:
a; \(\dfrac{-9}{4}\) < 0; \(\dfrac{1}{3}\) > o
\(\dfrac{-9}{4}\) < \(\dfrac{1}{3}\)
b; \(\dfrac{-8}{3}\) < - 1
\(\dfrac{4}{-7}\) > - 1
Vậy \(\dfrac{-8}{3}\) < \(\dfrac{4}{-7}\)
c; \(\dfrac{9}{-5}\) < - 1
\(\dfrac{7}{-10}\) > - 1
Vậy \(\dfrac{9}{-5}\) < \(\dfrac{7}{-10}\)
Đúng 2
Bình luận (0)
Câu 2:
a; Viết các phân số theo thứ tự tăng dần
\(\dfrac{-1}{2}\); \(\dfrac{2}{7}\); \(\dfrac{2}{5}\)
b; \(\dfrac{-11}{4}\); \(\dfrac{-7}{3}\); \(\dfrac{12}{5}\)
Đúng 2
Bình luận (0)
\(\dfrac{1}{3}\) = \(\dfrac{8}{24}\); \(\dfrac{1}{8}\) = \(\dfrac{3}{24}\); \(\dfrac{1}{6}\) = \(\dfrac{4}{24}\); \(\dfrac{1}{12}\) = \(\dfrac{2}{24}\); \(\dfrac{7}{24}\)
Hà giành thời gian nhiều nhất cho hoạt động Ngủ
Hà giành thời gian ít nhất cho hoạt động Ăn
Các phân số trong hình vẽ được sắp xếp theo thứ tự giảm dần là:
\(\dfrac{1}{3}\); \(\dfrac{7}{24}\); \(\dfrac{1}{6}\); \(\dfrac{1}{8}\); \(\dfrac{1}{12}\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Giúp mình câu 8, 9, 10, 11 với ạ. Mình cảm ơn nhiều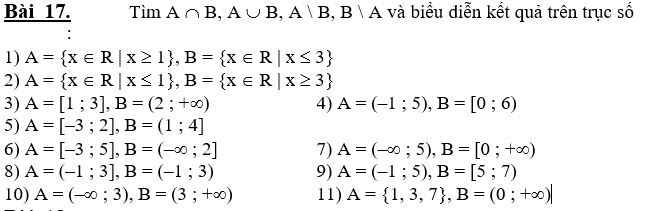
\(8,\\ A=\left\{0;1;2;3\right\}\\ B=\left\{0;1;2\right\}\\ A\cap B=\left\{0;1;2\right\}\\ A\cup B=\left\{0;1;2;3\right\}\\ A\B=\left\{3\right\}\\ B\A=\varnothing\\ 9,\\ A=\left\{0;1;2;3;4\right\}\\ B=\left\{5;6\right\}\\ A\cap B=\varnothing\\ A\cup B=\left\{0;1;2;3;4;5;6\right\}\\ A\B=\left\{0;1;2;3;4\right\}\\ B\A=\left\{5;6\right\}\)
Đúng 1
Bình luận (0)
8: \(A\cap B=\left\{3\right\}\)
\(A\cup B\)=(-1;3]
Đúng 0
Bình luận (0)
giải giúp mình từ câu f đến hết ạ mình cảm ơn hứa rate 5 sao ạ
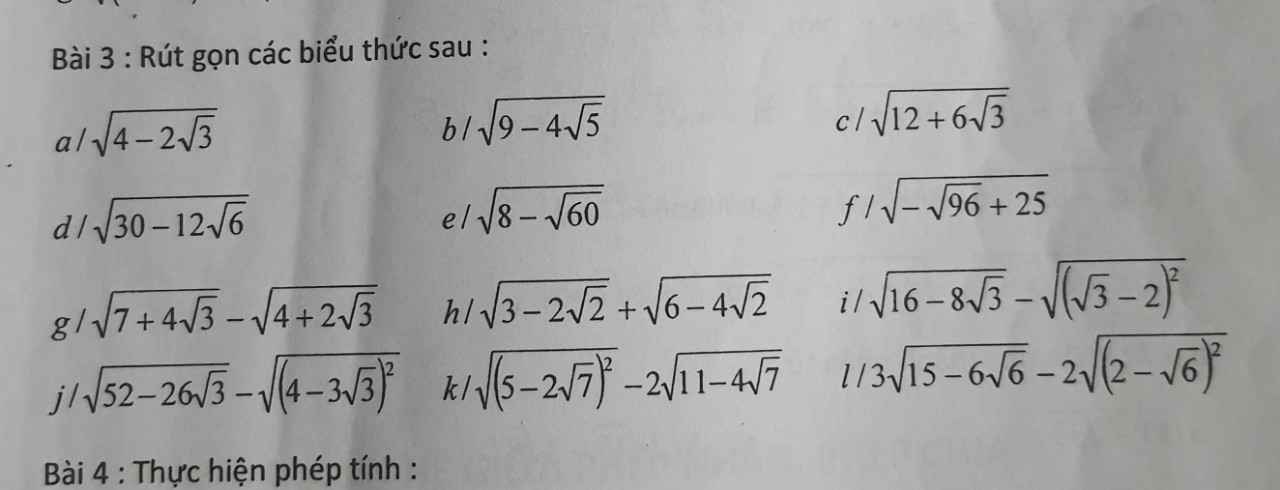
a) \(\sqrt{4-2\sqrt{3}}=\sqrt{3}-1\)
b) \(\sqrt{9-4\sqrt{5}}=\sqrt{10}-1\)
c) \(\sqrt{12+6\sqrt{3}}=3+\sqrt{3}\)
d) \(\sqrt{30-12\sqrt{6}}=3\sqrt{2}-2\sqrt{3}\)
e) \(\sqrt{8-\sqrt{60}}=\sqrt{5}-\sqrt{3}\)
f) \(\sqrt{-\sqrt{96}+25}=2\sqrt{6}-1\)
Đúng 1
Bình luận (1)
g: Ta có: \(\sqrt{7+4\sqrt{3}}-\sqrt{4+2\sqrt{3}}\)
\(=2+\sqrt{3}-\sqrt{3}-1\)
=1
h: Ta có: \(\sqrt{3-2\sqrt{2}}+\sqrt{6-4\sqrt{2}}\)
\(=\sqrt{2}-1+2-\sqrt{2}\)
=1
Đúng 0
Bình luận (0)
Mọi người giải giúp mình câu 3 với ạ, mình cảm ơn nhiều 
Giải giúp mình câu 5 với ạ , cảm ơn nhiều 
5:
Chiều rộng là (36-6):2=15(m)
Chiều dài là 15+6=21m
S=15*21=315m2
Đúng 0
Bình luận (0)
mọi người ơi giúp mình câu này với ạ, lời giải chi tiết càng tốt ạ, mình khá rối với câu này -.- cảm ơn mọi người nhiều
\(y'=\dfrac{\left(-2x+2\right)\left(x-3\right)-\left(-x^2+2x+c\right)}{\left(x-3\right)^2}=\dfrac{-x^2+6x-6-c}{\left(x-3\right)^2}\)
\(\Rightarrow\) Cực đại và cực tiểu của hàm là nghiệm của: \(-x^2+6x-6-c=0\) (1)
\(\Delta'=9-\left(6+c\right)>0\Rightarrow c< 3\)
Gọi \(x_1;x_2\) là 2 nghiệm của (1) \(\Rightarrow\left\{{}\begin{matrix}-x_1^2+6x_1-6=c\\-x_2^2+6x_2-6=c\end{matrix}\right.\)
\(\Rightarrow m-M=\dfrac{-x_1^2+2x_1+c}{x_1-3}-\dfrac{-x_2^2+2x_2+c}{x_2-3}=4\)
\(\Leftrightarrow\dfrac{-2x_1^2+8x_1-6}{x_1-3}-\dfrac{-2x_2^2+8x_2-6}{x_2-3}=4\)
\(\Leftrightarrow2\left(1-x_1\right)-2\left(1-x_2\right)=4\)
\(\Leftrightarrow x_2-x_1=2\)
Kết hợp với Viet: \(\left\{{}\begin{matrix}x_2-x_1=2\\x_1+x_2=6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_1=2\\x_2=4\end{matrix}\right.\)
\(\Rightarrow c=2\)
Có 1 giá trị nguyên
Đúng 0
Bình luận (0)
Ai giải hộ mình câu 10 và 11 với! Mik cảm ơn nhiều ạ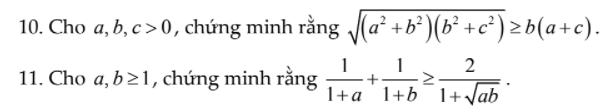 !
!
10. Câu này chứng minh BĐT BSC:
\(\sqrt{\left(a^2+b^2\right)\left(b^2+c^2\right)}\ge\sqrt{\left(ab+bc\right)^2}=b\left(a+c\right)\)
Đúng 1
Bình luận (0)
11.
Ta có: \(\dfrac{1}{1+a}+\dfrac{1}{1+b}-\dfrac{2}{1+\sqrt{ab}}\)
\(=\dfrac{\left(1+b\right)\left(1+\sqrt{ab}\right)}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}+\dfrac{\left(1+a\right)\left(1+\sqrt{ab}\right)}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}-\dfrac{2\left(1+a\right)\left(1+b\right)}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}\)
\(=\dfrac{1+b+\sqrt{ab}+b\sqrt{ab}}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}+\dfrac{1+a+\sqrt{ab}+a\sqrt{ab}}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}-\dfrac{2+2a+2b+2ab}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}\)
\(=\dfrac{-a-b+2\sqrt{ab}+a\sqrt{ab}+b\sqrt{ab}-2ab}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}\)
\(=\dfrac{\left(\sqrt{a}-\sqrt{b}\right)^2\left(\sqrt{ab}-1\right)}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}\ge0\forall x,y\ge1\)
Đẳng thức xảy ra khi \(a=b=1\)
Đúng 0
Bình luận (0)
Giải giúp mình câu 6vaf câu 7 với ạ. Cảm ơn mọi người rất nhiều
Ai giải hộ mình câu 10 và 11 với! Mik cảm ơn rất nhiều ạ.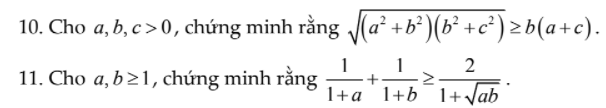
dùng phương pháp hình học cm câu a
đặt BH =a , HC =c kẻ HA =b
theo định lí py ta go ta có
AB=a2+b2;AC=b2+c2;BC=a+b
dễ thấy AB.AC\(\ge\) 2SABC=BC.AH
(a2+b2).(b2+c2)\(\ge\)b.(a+c)
Đúng 0
Bình luận (0)





















