Cho hình vẽ dưới đây với B A H ^ = A C H ^
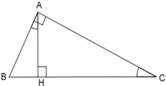
Khi đó các mệnh đề
(I) ΔAHB ~ ΔCHA (g - g)
(II) ΔAHC ~ ΔBAC (g - g)
A. (I) đúng
B. (II) đúng
C. Cả (I) và (II) đều sai
D. Cả (I) và (II) đều đúng
Vẽ hình theo trình tự sau:
- Vẽ tam giác ABC
- Vẽ đường thẳng đi qua A vuông góc với BC tại H
- Vẽ đường thẳng đi qua H vuông góc với AC tại T
- Vẽ đường thẳng đi qua T song song với BC
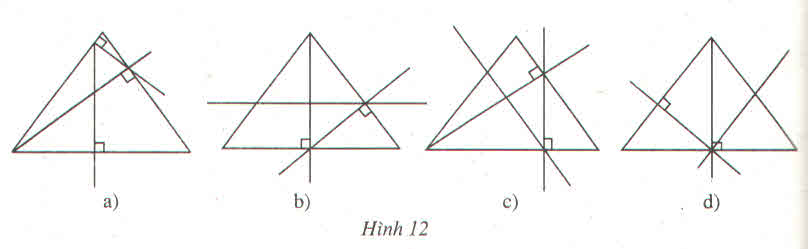
Trong các hình a,b,c,d dưới đây thì những hình nào vẽ đúng đề bài trên, hãy điền tên các điểm (theo đề bài) cho các hình vẽ đúng.
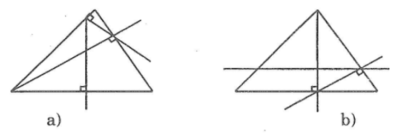
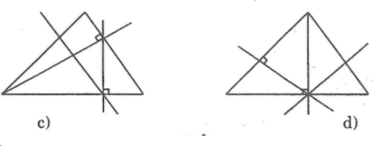
Hình a sai ; Hình b đúng ; Hình c đúng ; Hình d sai
Tên các điểm được thể hiện trong hình dưới:
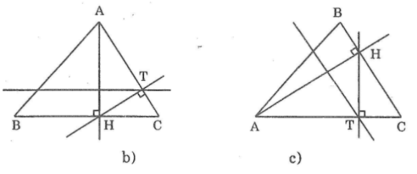
Vẽ hình theo trình tự sau :
- Vẽ tam giác ABC
- Vẽ đường thẳng đi qua A vuông góc với BC tại H
- Vẽ đường thẳng đi qua H vuông góc với AC tại T
- Vẽ đường thẳng đi qua T song song với BC
Trong các hình 12 a, b, c, d dưới đây thì những hình nào vẽ đúng đề bài trên. Hãy điền tên các điểm (theo đề bài) cho các hình vẽ đúng ?
Cho hình vẽ như dưới đây. Hỏi AH là đường cao của tam giác nào? Tính diện tích tam giác đó. Biết CH=3 cm; HM=4cm; MB=6cm; Ah=5cm.
Nhìn hình vẽ,ta thấy AH là đường cao của những tam giác ACH,AMH,ABH và ABC
Diện tích tam giác ACH:
\(\dfrac{3\times5}{2}=7,5\left(cm^2\right)\)
Diện tích tam giác AMH:
\(\dfrac{4\times5}{2}=10\left(cm^2\right)\)
Độ dài HB:
\(4+6=10\left(cm\right)\)
Diện tích tam giác AHB:
\(\dfrac{5\times10}{2}=25\left(cm^2\right)\)
Độ dài BC:
\(10+3=13\left(cm\right)\)
Diện tích tam giác ABC:
\(\dfrac{13\times5}{2}=32,5\left(cm^2\right)\)
\(AH\) là đường cao của tam giác \(AHC;AHM;AHB;ABC;ACM\)
\(S_{\Delta AHC}=\dfrac{CH\times AH}{2}=\dfrac{3\times5}{2}=7,5\left(cm^2\right)\)
\(S_{\Delta AHM}=\dfrac{AH\times HM}{2}=\dfrac{5\times4}{2}=10\left(cm^2\right)\)
\(HB=HM+MB=4+6=10\left(cm\right)\)
\(S_{\Delta AHB}=\dfrac{AH\times HB}{2}=\dfrac{5\times10}{2}=25\left(cm^2\right)\)
\(BC=HB+CH=10+3=13\left(cm\right)\)
\(S_{\Delta ABC}=\dfrac{AH\times BC}{2}=\dfrac{5\times13}{2}=32,5\left(cm^2\right)\)
\(MC=CH+HM=3+4=7\left(cm\right)\)
\(S_{\Delta ACM}=\dfrac{AH\times MC}{2}=\dfrac{5\times7}{2}=17,5\left(cm^2\right)\)
Cho hình h tạo bởi hai hình chữ nhật như hình vẽ dưới đây. Tính diện tích hình H.
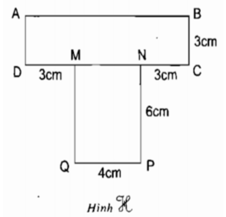
Độ dài cạnh DC= DM + MN + NC là:
3 + 4 + 3 = 10 (cm)
Diệc tích hình chữ nhật ABCD là:
10 × 3 = 30 ( c m 2 )
Diện tích hình chữ nhật NMPQ là:
4 × 6 = 24 ( c m 2 )
Diện tích hình H là:
30 + 24 = 54 ( c m 2 )
Đáp số: 54 ( c m 2 )
Trong không gian với hệ tọa độ Oxyz cho S(-1;6;2), A(0;0;6), B(0;3;0), C(-2;0;0). Gọi H là chân đường cao vẽ từ S của tứ diện. Phương trình nào dưới đây là phương trình mặt phẳng (SBH) ?
A. x + 5y - 7z - 15 = 0
B. 5x - y + 7z + 15 = 0
C. 7z + 5y + z - 15 = 0
D. x - 7y + 5z + 15 = 0
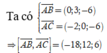 là một VTPT của mp (ABC)
là một VTPT của mp (ABC)
![]() nên mp (SBH) có một VTPT là
nên mp (SBH) có một VTPT là ![]()
Vậy mp (SBH) đi qua điểm B(0;3;0) và có một VTPT ![]()
nên có phương trình x + 5y - 7z - 15 = 0. Chọn A.
Cho hình bình hành . Điểm đối xứng với điểm qua điểm , điểm đối xứng với điểm qua điểm , điểm đối xứng với điểm qua . Nhận định nào dưới đây đúng?
A. Điểm đối xứng với điểm qua . B. là tâm đối xứng của hình .
C. là hình bình hành. D. Tất cả đáp án trên.
cho tam giác A B C vuông tại A.Kẻ A H vuông góc với B C (H € BC)
a)tìm các cặp góc phụ nhau trong hình vẽ
b)tìm các cặp góc nhọn bằng nhau trong hình vẽ
Cho hình H tạo bởi 2 hình chữ nhật như hình vẽ dưới đây .
Tính diện tích hình H.
bạn ơi, nếu bạn ko vẽ hình ra thì m.n ko biết làm thế nào đâu!
hothiluuphuc đã hỏi về một câu hỏi ngớ ngẩn hết mức cho phép rùi bà con ơi .
TỚ KHÔNG BIẾT TRẢ LỜI NẾU MÀ KHÔNG CÓ HÌNH BẠN Ạ .
THẬT ĐÁNG TIẾC , LÀM ƠN TẢI HÌNH LÊN GIÚP MÌNH NHÉ .
Cho hàm số y=f(x)= a x 3 + b x 2 + c x + d , ( a , b , c , d ∈ R , a khác 0) có đồ thị (C). Biết rằng đồ thị (C) tiếp xúc với đường thẳng y = 4 tại điểm có hoành độ âm và đồ thị của hàm số y= f ' ( x ) cho bởi hình vẽ dưới đây. Tính thể tích vật thể tròn xoay được tạo thành khi quay hình phẳng H giời hạn bởi đồ thị (C) và trục hoành xung quanh trục hoành Ox
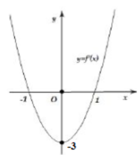
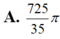
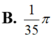
![]()
![]()
Câu 4:Cho hình H tạo bởi hình chữ nhật như hình vẽ dưới đây. Tính diện tích hình
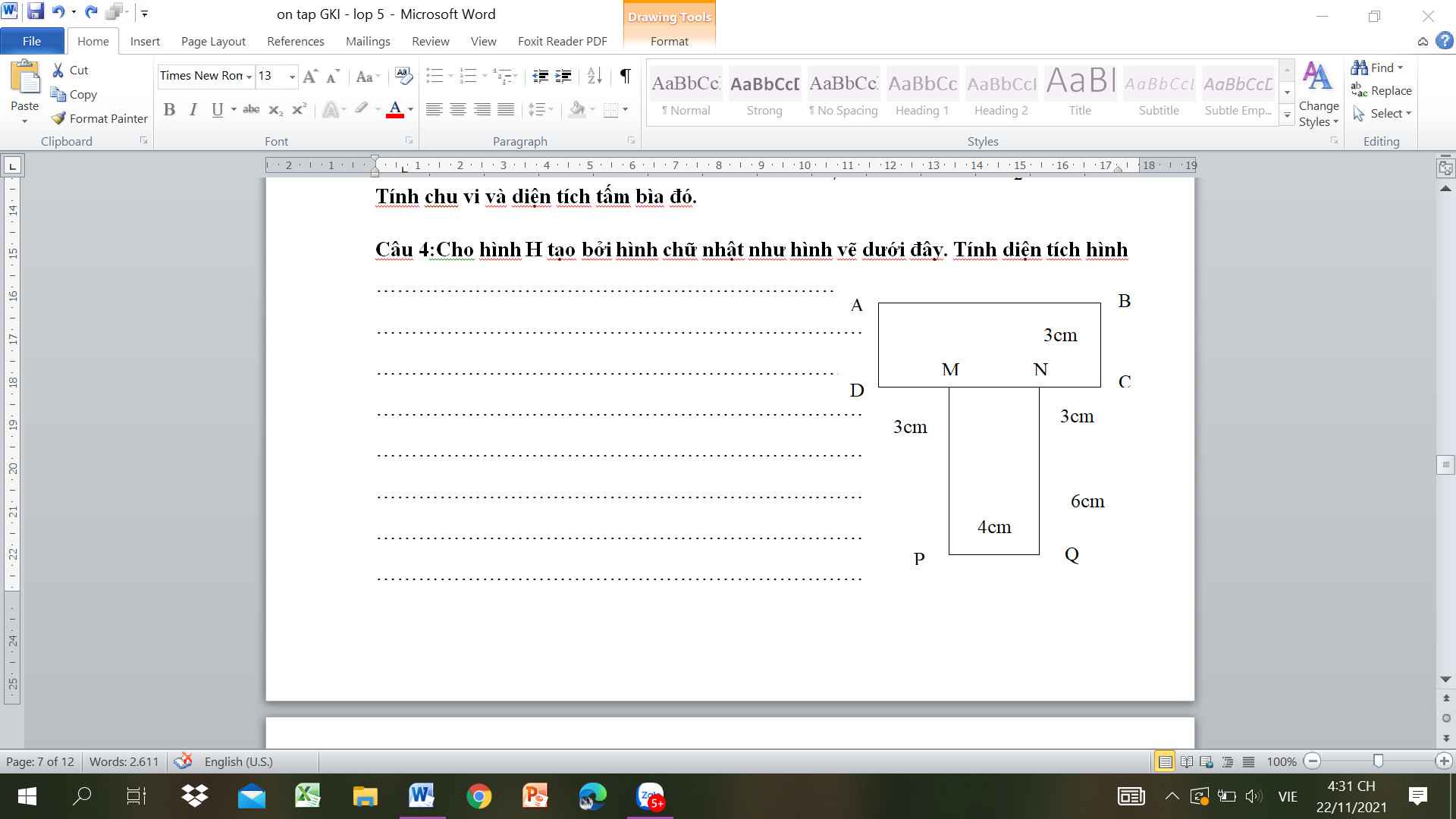
\(S_{ADMPQNCB}=S_{ABCD}+S_{MNPQ}=3\times\left(3+4+3\right)+4\times6=54\left(cm^2\right)\)