Chọn kết quả đúng:
Giá trị của biểu thức x 2 – x y + x tại x = 100 và y = 11 là:
A. 990
B. 9900
C. 9000
D. 1100
Câu 6. Kết quả của
Tùy chọn 1
Tùy chọn 2
Tùy chọn 3
Kết quả khác
Câu 7. Kết quả thu gọn của biểu thức
Tùy chọn 1
Tùy chọn 2
Tùy chọn 3
Tùy chọn 4
Câu 8. Biểu thức sau có nghĩa khi x ....
Với mọi giá trị của x
Tùy chọn 2
Tùy chọn 3
Tùy chọn 4
Câu 9. Phân tích thành nhân tử
Tùy chọn 1
Tùy chọn 2
Tùy chọn 3
đáp án khác
Câu 10. Tính
1600
200
40
-400
mọi người ơi,tùy chọn bên dưới là kết quả bên trên nha!
6) \(\sqrt{\left(2-\sqrt{5}\right)^2}=\left|2-\sqrt{5}\right|=\sqrt{5}-2\) =>Chọn 2
7) \(\sqrt{4\left(a-2\right)^2}=2\left|a-2\right|=2\left(2-a\right)\)( do \(a\le2\)) => Chọn 3
8) Để \(\sqrt{4+a^2}\) thì \(4+a^2\ge0\left(đúng\forall a\right)\) => Chọn 1
9) \(x^2-7=\left(x-\sqrt{7}\right)\left(x+\sqrt{7}\right)\) => Chọn 3
10) \(\sqrt{\left(-25\right)\left(-64\right)}=\sqrt{25.64}=\sqrt{25}.\sqrt{64}=5.8=40\)=> Chọn 3
Chọn kết quả đúng: Cho biểu thức M = 2 x + 1 x + 1 + x - 3 x + 3 . Để M = 3 thì giá trị của x là:
A. - 9 7
B. - 9 17
C. 9 7
D. 5 7
Điền kết quả tính được vào bảng:
| Giá trị của x và y | Giá trị biểu thức (x – y)(x2 + xy + y2) |
| x = -10 ; y = 2 | |
| x = -1 ; y = 0 | |
| x = 2 ; y = -1 | |
| x = -0,5 ; y = 1,25 |
Ta có:
A = (x – y).(x2 + xy + y2)
= x.(x2 + xy + y2) + (–y).(x2 + xy + y2)
= x.x2 + x.xy + x.y2 + (–y).x2 + (–y).xy + (–y).y2
= x3 + x2y + xy2 – x2y – xy2 – y3
= x3 – y3 + (x2y – x2y) + (xy2 – xy2)
= x3 – y3.
Tại x = –10, y = 2 thì A = (–10)3 – 23 = –1000 – 8 = –1008
Tại x = –1 ; y = 0 thì A = (–1)3 – 03 = –1 – 0 = –1
Tại x = 2 ; y = –1 thì A = 23 – (–1)3 = 8 – (–1) = 9
Tại x = –0,5 ; y = 1,25 thì A = (–0,5)3 – 1,253 = –0,125 – 1,953125 = –2,078125
Vậy ta có bảng sau :
| Giá trị của x và y | Giá trị biểu thức (x – y)(x2 + xy + y2) |
| x = -10 ; y = 2 | -1008 |
| x = -1 ; y = 0 | -1 |
| x = 2 ; y = -1 | 9 |
| x = -0,5 ; y = 1,25 | -2,078125 |
Giá trị của biểu thức 3.(7x-2x-2/3y+7/9y) tại x=-1/10;y=4,8 là (Nhập kết quả dưới dạng số thập phân gọn nhất)?
a) tính giá trị của biểu thức: x^2+2y tại x=2, y= –3 b) tính giá trị của biểu thức: x^2+2xy+y^2 tại x=4, y=6 c) tính giá trị của biểu thức: P= x^2-4xy+4y^2 tại x=1 và y= 1/2
a: Khi x=2 và y=-3 thì \(x^2+2y=2^2+2\cdot\left(-3\right)=4-6=-2\)
b: \(A=x^2+2xy+y^2=\left(x+y\right)^2\)
Khi x=4 và y=6 thì \(A=\left(4+6\right)^2=10^2=100\)
c: \(P=x^2-4xy+4y^2=\left(x-2y\right)^2\)
Khi x=1 và y=1/2 thì \(P=\left(1-2\cdot\dfrac{1}{2}\right)^2=\left(1-1\right)^2=0\)
Rút gọn biểu thức x(x − y) − y(y − x) ta được ?
(A) x 2 + y 2
(B) x 2 - y 2
(C) x 2 - x y
(D) x - y 2
Hãy chọn kết quả đúng.
Ta có:
x x - y - y y - x = x 2 - x y - y 2 - x y = x 2 - x y - y 2 + x y = x 2 - y 2
Chọn (B) x 2 - y 2
Chọn kết luận đúng về giá trị của biểu thức
E = 2 3 x 2 y 3 : ( ( - 1 ) 3 x y ) + ( 2 x ( y - 1 ) ( y + 1 ) 2 ) y + 1 (x ≠ 0, y ≠ 0, y ≠ -1)
A. Giá trị của biểu thức không phụ thuộc biến x
B. Giá trị của biểu thức không phụ thuộc biến y
C. Giá trị của biểu thức không phụ thuộc biến
D. Giá trị của biểu thức không phụ thuộc vào cả hai biến x, y
E = 2 3 x 2 y 3 : ( ( - 1 ) 3 x y ) + ( 2 x ( y - 1 ) ( y + 1 ) 2 ) y + 1 ⇔ E = - 2 x y 2 + 2 x ( y – 1 ) ( y + 1 ) ⇔ E = - 2 x y 2 + 2 x ( y 2 – 1 ) ⇔ E = - 2 x y 2 + 2 x y 2 – 2 x
ó E = -2x
Vậy Giá trị của biểu thức E không phụ thuộc biến y
Đáp án cần chọn là: B
Bài 3:
a) Tính giá trị của biểu thức tại P = x(x - y) + y(x - y) tại x = 5 và y = 4;
b) Tính giá trị của biểu thức tại Q = x(x2 - y) - x2(x + y) + y(x2 - x) tại x = 1/2 và y = -100;
a) \(P=x\left(x-y\right)+y\left(x-y\right)=\left(x-y\right)\left(x+y\right)=x^2-y^2=5^2-4^2=9\)
b) \(Q=x\left(x^2-y\right)-x^2\left(x+y\right)+y\left(x^2-x\right)=x^3-xy-x^3-x^2y+x^2y-xy=0\)
a) Biểu diễn miền nghiệm D của bất phương trình bậc nhất hai ẩn sau:
\(\left\{ \begin{array}{l}x - y \le 6\\2x - y \le 2\\x \ge 0\\y \ge 0\end{array} \right.\)
b) Từ kết quả câu a, tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức \(F(x;y) = 2x + 3y\) trên miền D.
+ Biểu diễn miền nghiệm của BPT \(x - y \le 6\)
Bước 1: Vẽ đường thẳng \(d:x - y = 6\) trên mặt phẳng tọa độ Õy
Bước 2: Lấy O(0;0) không thuộc d, ta có: \(0 - 0 = 0 \le 6\) => điểm O(0;0) thuộc miền nghiệm
=> Miền nghiệm của BPT \(x - y \le 6\) là nửa mp bờ d, chứa gốc tọa độ.
+ Tương tự, ta có miền nghiệm của BPT \(2x - y \le 2\) là nửa mp bờ \(d':2x - y = 0\), chứa gốc tọa độ.
+ Miền nghiệm của BPT \(x \ge 0\) là nửa mp bên phải Oy (tính cả trục Oy)
+ Miền nghiệm của BPT \(y \ge 0\) là nửa mp phía trên Ox (tính cả trục Ox)
Biểu diễn trên cùng một mặt phẳng tọa độ và gạch bỏ các miền không là nghiệm của từng BPT, ta được:
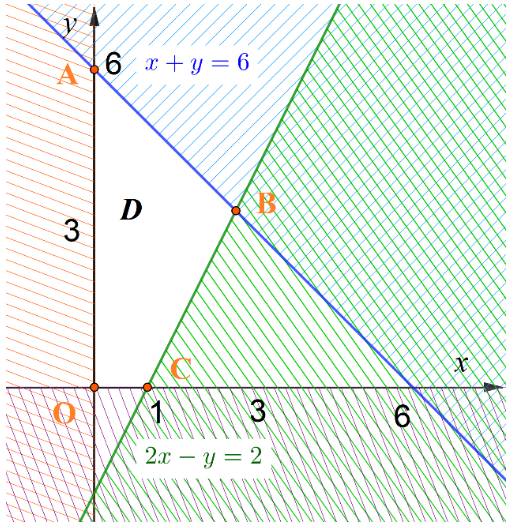
Miền nghiệm của hệ bất phương trình đã cho là miền tứ giác OABC (miền không bị gạch) với \(A(0;6),B(\frac{8}{3};\frac{{10}}{3}),C(1;0)\)
b)
Thay tọa độ các điểm \(O(0;0),A(0;6),B(\frac{8}{3};\frac{{10}}{3}),C(1;0)\) và biểu thức \(F(x;y) = 2x + 3y\) ta được:
\(\begin{array}{l}F(0;0) = 2.0 + 3.0 = 0\\F(0;6) = 2.0 + 3.6 = 18\\F(\frac{8}{3};\frac{{10}}{3}) = 2.\frac{8}{3} + 3.\frac{{10}}{3} = \frac{{46}}{3}\\F(1;0) = 2.1 + 3.0 = 2\end{array}\)
\( \Rightarrow \min F = 0\), \(\max F = 18\)
Vậy trên miền D, giá trị nhỏ nhất của F bằng 0, giá trị lớn nhất của F bằng \(18\).