y=√(cosx-1):(4+cosx)

Những câu hỏi liên quan
Xét tính chẵn, lẻ của các hàm số1,ycosx+sin^2x2,ysinx+cosx3,ytanx+2sinx4,ytan2x-sin3x5,sin2x+cosx6,ycosx.sin^2x-tan^2x7,ycosleft(x-dfrac{pi}{4}right)+cosleft(x+dfrac{pi}{4}right)8,ydfrac{2+cosx}{1+sin^2x}9,yleft|2+sinxright|+left|2-sinxright|
Đọc tiếp
Xét tính chẵn, lẻ của các hàm số
1,\(y=cosx+sin^2x\)
2,\(y=sinx+cosx\)
3,\(y=tanx+2sinx\)
4,\(y=tan2x-sin3x\)
5,\(sin2x+cosx\)
6,\(y=cosx.sin^2x-tan^2x\)
7,\(y=cos\left(x-\dfrac{\pi}{4}\right)+cos\left(x+\dfrac{\pi}{4}\right)\)
8,\(y=\dfrac{2+cosx}{1+sin^2x}\)
9,\(y=\left|2+sinx\right|+\left|2-sinx\right|\)
Cho hàm số
y
1
+
sin
x
1
+
cos
x
. Xét hai kết quả:(I)
y
(
cos
x
-
sin
x
)
(
1
+
cos
x
+...
Đọc tiếp
Cho hàm số y = 1 + sin x 1 + cos x . Xét hai kết quả:
(I) y ' = ( cos x - sin x ) ( 1 + cos x + sin x ) 1 + cos x 2
(II) y ' = 1 + cos x + sin x 1 + cos x 2
Kết quả nào đúng?
A. Cả hai đều sai.
B. Chỉ (II).
C. Chỉ (I).
D. Cả hai đều đúng.
- Ta có :
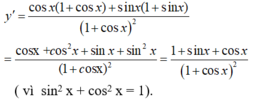
+) Xét (I) ta có:
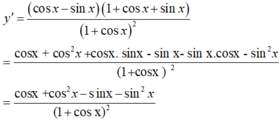
+) Do đó, (I) đúng và (II) sai.
Chọn B.
Đúng 0
Bình luận (0)
Cho hàm số
y
1
+
sin
x
1
+
cos
x
. Xét hai kết quả:(I)
y
(
cos
x
-
sin
x
)
(
1
+
cos
x
+...
Đọc tiếp
Cho hàm số y = 1 + sin x 1 + cos x . Xét hai kết quả:
(I) y ' = ( cos x - sin x ) ( 1 + cos x + sin x ) 1 + cos x 2
(II) y ' = 1 + cos x + sin x 1 + cos x 2
Kết quả nào đúng?
A. Cả hai đều sai.
B. Chỉ (II).
C. Chỉ (I).
D. Cả hai đều đúng.
- Ta có :
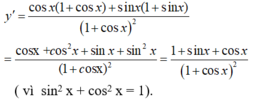
+) Xét (I) ta có:
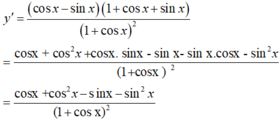
+) Do đó, (I) đúng và (II) sai.
Chọn B.
Đúng 0
Bình luận (0)
y=\(\dfrac{sinx+cosx}{4+sinx-cosx}\)
\(\Rightarrow4y+y.sinx-y.cosx=sinx+cosx\)
\(\Leftrightarrow\left(1-y\right)sinx+\left(1+y\right)cosx=4y\)
Theo điều kiện có nghiệm của pt lượng giác bậc nhất:
\(\left(1-y\right)^2+\left(1+y\right)^2\ge\left(4y\right)^2\)
\(\Leftrightarrow14y^2\le2\)
\(\Leftrightarrow-\dfrac{\sqrt{7}}{7}\le y\le\dfrac{\sqrt{7}}{7}\)
Đúng 3
Bình luận (0)
Tìm tập xác định của các hàm số sau:1,ysindfrac{3x+2}{2x-1}2,ytanleft(3x+dfrac{2pi}{5}right)3,ycotleft(2x-dfrac{1}{3}right)4,ydfrac{sinx+cosx}{sinx-cosx}5,ydfrac{1}{sinx}+dfrac{1}{cosx}6,ydfrac{sqrt{1-sinx}}{cosx}7,ydfrac{3}{sin^2x-cos^2x}8,ydfrac{1+tanx}{1+sinx}9,ysqrt{dfrac{1+sinx}{1-cosx}}
Đọc tiếp
Tìm tập xác định của các hàm số sau:
1,\(y=sin\dfrac{3x+2}{2x-1}\)
2,\(y=tan\left(3x+\dfrac{2\pi}{5}\right)\)
3,\(y=cot\left(2x-\dfrac{1}{3}\right)\)
4,\(y=\dfrac{sinx+cosx}{sinx-cosx}\)
5,\(y=\dfrac{1}{sinx}+\dfrac{1}{cosx}\)
6,\(y=\dfrac{\sqrt{1-sinx}}{cosx}\)
7,\(y=\dfrac{3}{sin^2x-cos^2x}\)
8,\(y=\dfrac{1+tanx}{1+sinx}\)
9,\(y=\sqrt{\dfrac{1+sinx}{1-cosx}}\)
Tìm TXĐ của các hàm số saua,dfrac{1-cosx}{2sinx+1}b,ysqrt{dfrac{1+cosx}{2-cosx}}c,sqrt{tanx}d,dfrac{2}{2cosleft(x-dfrac{Pi}{4}right)-1}e,tanleft(x-dfrac{Pi}{3}right)+cotleft(x+dfrac{Pi}{4}right)f,ydfrac{sinx}{cos^2x-sin^2x}g,ydfrac{2}{cosx+cos2x}h,ydfrac{1+cos2x}{1-cos4x}
Đọc tiếp
Tìm TXĐ của các hàm số sau
\(a,\dfrac{1-cosx}{2sinx+1}\)
\(b,y=\sqrt{\dfrac{1+cosx}{2-cosx}}\)
\(c,\sqrt{tanx}\)
\(d,\dfrac{2}{2cos\left(x-\dfrac{\Pi}{4}\right)-1}\)
\(e,tan\left(x-\dfrac{\Pi}{3}\right)+cot\left(x+\dfrac{\Pi}{4}\right)\)
\(f,y=\dfrac{sinx}{cos^2x-sin^2x}\)
\(g,y=\dfrac{2}{cosx+cos2x}\)
\(h,y=\dfrac{1+cos2x}{1-cos4x}\)
a: ĐKXĐ: 2*sin x+1<>0
=>sin x<>-1/2
=>x<>-pi/6+k2pi và x<>7/6pi+k2pi
b: ĐKXĐ: \(\dfrac{1+cosx}{2-cosx}>=0\)
mà 1+cosx>=0
nên 2-cosx>=0
=>cosx<=2(luôn đúng)
c ĐKXĐ: tan x>0
=>kpi<x<pi/2+kpi
d: ĐKXĐ: \(2\cdot cos\left(x-\dfrac{pi}{4}\right)-1< >0\)
=>cos(x-pi/4)<>1/2
=>x-pi/4<>pi/3+k2pi và x-pi/4<>-pi/3+k2pi
=>x<>7/12pi+k2pi và x<>-pi/12+k2pi
e: ĐKXĐ: x-pi/3<>pi/2+kpi và x+pi/4<>kpi
=>x<>5/6pi+kpi và x<>kpi-pi/4
f: ĐKXĐ: cos^2x-sin^2x<>0
=>cos2x<>0
=>2x<>pi/2+kpi
=>x<>pi/4+kpi/2
Đúng 0
Bình luận (0)
cíuuuuuuu em với phần đạo hàm cấp n của các hàm số sau:
1.\(y=sinax\) 2.\(y=cosax\)
\(3.y=sin3x\cdot cosx\) \(4.y=cos5x\cdot cosx\)
Cho hàm số: y = ex cosx Khi đó: y'/ex?
A. cosx - sinx
B. sinx - cosx
C. sinx + cosx
D. cosx
\(y'=\left(e^x\right)'.cosx+e^x.\left(cosx\right)'=e^x\left(cosx-sinx\right)\)
=> Chọn A
Đúng 0
Bình luận (0)
1) y = \(\frac{cosx+1}{cosx}\)
2) y = \(\frac{4-cosx}{\sqrt{1-sinx}}\)
3) y = 3 - |\(sinx\)|
-
Mọi người giúp mình với ạ.
ĐKXĐ:
a. \(cosx\ne0\Leftrightarrow x\ne\frac{\pi}{2}+k\pi\)
b. \(sinx\ne1\Leftrightarrow x\ne\frac{\pi}{2}+k2\pi\)
c. Hàm luôn xác định với mọi x
Đúng 0
Bình luận (0)
Đề bài yêu cầu là gì bạn? Bạn không nêu yêu cầu thì làm sao biết để giúp ạ?
Đúng 0
Bình luận (0)


















