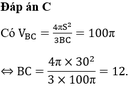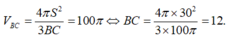cho tam giác ABC có góc Bằng 45 độ, góc C bằng 30 độ cạnh BC bằng 8cm. Tính diện tích tam giác ABC

Những câu hỏi liên quan
cho tam giác vuông ABC , biết độ dài cạnh huyền bằng 8cm , hiệu 2 cạnh góc vuông bằng 4cm . Tính diện tích tam giác vuông ABC
Gọi độ dài cạnh góc vuông thứ nhất là x(cm)
=>Độ dài cạnh góc vuông thứ hai là x+4(cm)
Độ dài cạnh huyền là 8cm nên ta có: \(x^2+\left(x+4\right)^2=8^2\)
=>\(x^2+x^2+8x+16-64=0\)
=>\(2x^2+8x-48=0\)
=>\(x^2+4x-24=0\)
=>\(x^2+4x+4-28=0\)
=>\(\left(x+2\right)^2=28\)
=>\(\left[{}\begin{matrix}x+2=2\sqrt{7}\\x+2=-2\sqrt{7}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\sqrt{7}-2\left(nhận\right)\\x=-2\sqrt{7}-2\left(loại\right)\end{matrix}\right.\)
Độ dài cạnh góc vuông thứ hai là:
\(2\sqrt{7}-2+4=2\sqrt{7}+2\left(cm\right)\)
Diện tích tam giác vuông ABC là:
\(\dfrac{1}{2}\left(2\sqrt{7}-2\right)\left(2\sqrt{7}+2\right)\)
\(=\dfrac{1}{2}\left(28-4\right)\)
\(=\dfrac{1}{2}\cdot24=12\left(cm^2\right)\)
Đúng 0
Bình luận (0)
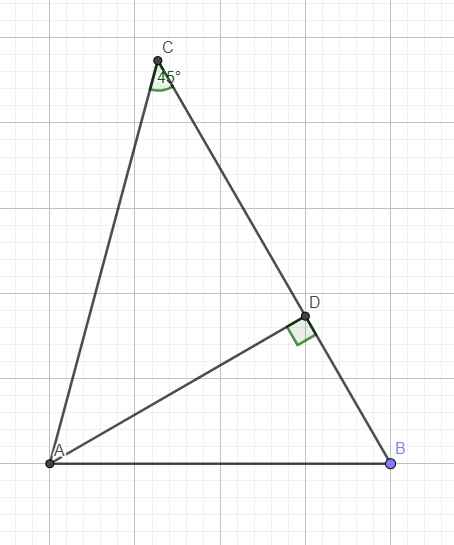
Cho tam giác ABC có góc C bằng 45 độ, AB. AC=32\(\sqrt{6}\), AB:AC=\(\sqrt{6}\):3. Tính BC, góc B và diện tích tam giác ABC
\(\dfrac{AB}{AC}=\dfrac{\sqrt{6}}{3}\Rightarrow AB=\dfrac{AC\sqrt{6}}{3}\)
\(AB.AC=32\sqrt{6}\Rightarrow\dfrac{AC^2\sqrt{6}}{3}=32\sqrt{6}\)
\(\Rightarrow AC^2=96\Rightarrow AC=4\sqrt{6}\)
\(\Rightarrow AB=\dfrac{AC\sqrt{6}}{3}=8\)
Kẻ đường cao AD ứng với BC
Do \(C=45^0\Rightarrow\widehat{CAD}=90^0-45^0=45^0\Rightarrow\Delta ACD\) vuông cân tại D
\(\Rightarrow AD=CD=\dfrac{AC}{\sqrt{2}}=4\sqrt{3}\)
Pitago tam giác vuông ABD:
\(BD=\sqrt{AB^2-AD^2}=4\)
\(\Rightarrow BC=CD+BD=4+4\sqrt{3}\)
\(cosB=\dfrac{BD}{AB}=\dfrac{4}{8}=\dfrac{1}{2}\Rightarrow B=60^0\)
\(S_{ABC}=\dfrac{1}{2}AD.BC=\dfrac{1}{2}.4\sqrt{3}.\left(4+4\sqrt{3}\right)=...\)
Đúng 0
Bình luận (0)
Giúp mình mới
1, Tính diện tích tấm giác biết độ dài 3 đường cao của tấm giác đó lần lượt là:60, 65, 156 cm
2, Tam giác ABC có đường BH bằng nửa cạnh BC. Góc A bằng 75 độ. Chứng minh tam giác ABC cân
3, Tam giác ABC có góc C bằng 90 độ, góc A bằng 30 độ, cạnh AC bằng 10 cm, CD vuông góc với AB (D thuộc AB), DE vuông góc với AC ( E thuộc AC). Tính cạnh AE
cho tam giác vuông ABC vuông tại A và M là trung điểm của BC, hãy chỉ ra cạnh huyền, cạnh góc vuông, trung tuyến ứng với cạnh huyền. A cho cạnh AB=9cm, AC=12cm. tính BC,MA, diện tích tam giác ABC,ABM? B cho góc B bằng 45 độ, tính góc C, chứng minh tam giác ABC vuông cân và AM vuông góc với bc. tính AM
Hãy cho tam giác abc có ab = 8cm góc b = 45 độ góc c bằng 60 độ kẻ đường cao ah của tam giác đó hãy tính ( làm tròn kết quả đến chữ số thập phân thứ 2)
A. Đường cao ah
B. Cạnh bc
Cho tam giác ABC có góc B = 60 độ , góc C bằng 40 độ , cso BC = 6cm . Tính
a) Đường cao AH và cạnh AC
b) Tính diện tích tam giác ABC
a) Ta có: \(BH+HC=BC\)
\(\Leftrightarrow AH\cdot\cot B+AH\cdot\cot C=BC\)
\(\Leftrightarrow AH\cdot\left(\frac{\sqrt{3}}{3}+1,3\right)=BC\)
\(\Leftrightarrow AH\cdot1,9=10\)
\(\Rightarrow AH=5,3\left(cm\right)\)
\(\Rightarrow AC=\frac{AH}{\sin C}=\frac{5,3}{0,6}=8,2\left(cm\right)\)
b) Ta có: \(S_{ABC}=\frac{AH\cdot BC}{2}=\frac{5,3\cdot10}{2}=26,5\left(cm^2\right)\)
P/s: Các kết quả chỉ tương đối
Cho tam giác ABC có độ dài cạnh AB bằng 6,4 cm, cạnh AC có độ dài 8cm. Góc B bằng hai lần góc C. Tính độ dài cạnh BC
Cho tam giác ABC có AB = 1 cm, AC = 2cm, góc ABC = 45 độ, góc ACB = 30 độ. Tính độ dài BC và diện tích tam giác ABC.
Cho tam giác ABC có diện tích bằng 30. Quay tam giác ABC quanh cạnh BC thu được vật thể tròn xoay có thể tích bằng 100 π . Tính độ dài cạnh BC.
A. 6.
B. 9.
C. 12.
D. 18.
Cho tam giác ABC có diện tích bằng 30. Quay tam giác ABC quanh cạnh BC thu được vật thể tròn xoay có thể tích bằng 100π . Tính độ dài cạnh BC. A. 6. B. 9. C. 12. D. 18.
Đọc tiếp
Cho tam giác ABC có diện tích bằng 30. Quay tam giác ABC quanh cạnh BC thu được vật thể tròn xoay có thể tích bằng 100π . Tính độ dài cạnh BC.
A. 6.
B. 9.
C. 12.
D. 18.