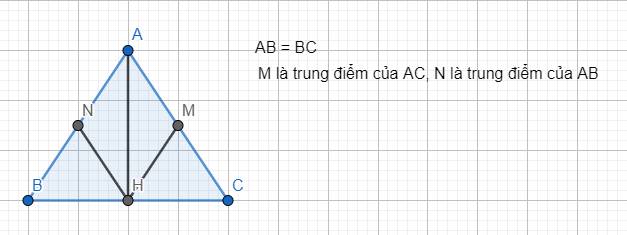
Cho tam giác ABC cân tại A có AH là đường cao (H thuộc BC). Gọi M,N lần lượt là trung điểm của AB và AC
a) Chứng minh 2 tam giác AHM và AHN bằng nhau (cạnh góc cạnh)
b) Chứng minh HM=HN
Câu a bạn có chép sai ko vậy?
Giải
b)Xét tam giác BAH và CAH có:
AB=AC(gt)
góc B =góc C(gt)
AH chung
\(\Rightarrow\)tam giác BAH =CAH (c.g.c)
\(\Rightarrow\)góc BAH=CAH (2 góc t/ư)
Mặt khác AH nằm giữa AB và AC ,chia góc A thành 2 góc bằng nhau
Mà H là trung điểm BC
\(\Rightarrow\)AH là tia phân giác góc A và vuông góc BC
a) Sửa đề: ΔAHB=ΔAHC
Xét ΔAHB và ΔAHC có
AH chung
AB=AC(ΔABC cân tại A)
HB=HC(H là trung điểm của BC)
Do đó: ΔAHB=ΔAHC(c-g-c)
Cho tam giác ABC cân tại A. Điểm H là trung điểm của cạnh BC.
a) Chứng minh tam giác ABH= tam giác ACH . Chứng minh AH vuông góc với BC.
b) Kẻ HM vuông góc với AB tại M, kẻ HN vuông góc với AC tại N. Chứng minh góc AHM= góc AHN
c) Gọi I là giao điểm của MH và AC, gọi K là giao điểm của NH và AB. Chứng minh tam giác AIK là tam giác cân.
XCho tam giác ABC cân tại A, đường cao AH (H thuộc BC)
a, Chứng minh Tam giác ABH= Tam giác ACH
b,Từ H kẻ MH, HN lần lượt vuông góc với AB và AC (M thuộc AB) (N thuộc AC). Chứng minh HM=HN
c, Gọi G là giao điểm của hai trung tuyến BE và CF của tam giác ABC (E thuộc AC) (F thuộc AB)
Làm nhanh mk tick!
a) Xét tam giác ABH vuông tại H và tam giác ACH vuông tại H có:
AB=AC(tam giác ABC cân tại A)
AH: chung
Do đó:tam giác ABH= tam giác ACH(ch-cgv)
b)Xét tam giác BMH vuông tại M và tam giác CNH vuông tại N có:
BH=CH(tam giác ABH=tam giác ACH)
góc B=góc C(tam giác ABC cân tại A)
Do đó:tam giác BMH=tam giác CNH(ch-gn)
#Ở câu b bạn có thể chọn trường hợp ch-cgv cũng đc hjhj:)))<3#
c)bn cho thiếu dữ kiên nên mk k làm đc nhé tks
P/S: chúc bạn học tốt..........boaiiii>.< moa<3
a) Xét ΔAHM vuông tại M và ΔAHN vuông tại N có
AH chung
\(\widehat{MAH}=\widehat{NAH}\)(AH là tia phân giác của \(\widehat{MAN}\))
Do đó: ΔAHM=ΔAHN(cạnh huyền-góc nhọn)
cho tam giác ABC cân tại A. Gọi H là trung điểm của BC
a) Chứng minh tam giác ABH=tam giác ACH
b)Gọi M là trung điểm của cạnh AC và N là trung điểm của cạnh AB. Chứng minh HN=HM
a, Xét tam giác \(\Delta ABH\) và \(\Delta ACH\) có :
\(HB=HC\left(gt\right)\)
\(\widehat{B}=\widehat{C}\left(gt\right)\)
\(AB=AC\left(gt\right)\)
= > \(\Delta ABH=\Delta ACH\left(c-g-c\right)\)
b, M là trung điểm của cạnh AC = > MA = 1/2 AC ( 1 )
N là trung điểm của cạnh AB = > NA = 1/2 AB ( 2 )
Từ ( 1 ) , ( 2 ) = > MA = NA ( Do AB = AC )
Mà tam giác ABH = tam giác ACH ( câu a, )
= > \(\widehat{BAH}=\widehat{CAH}\) ( 2 góc tương ứng )
Xét \(\Delta ANH\) và \(\Delta AMH\) có :
\(AN=AM\left(cmt\right)\)
\(\widehat{BAH}=\widehat{CAH}\left(cmt\right)\)
AH chung
= > \(\Delta ANH=\Delta AMH\left(c-g-c\right)\)
= > HN = HM ( 2 cạnh tương ứng )
a) Xét hai tam giác ABH và ACH ta có:
- AB = AC (vì ABC là tam giác cân)
- HB = HC (vì H là trung điểm của BC)
- \(\widehat{B}=\widehat{C}\) (vì ABC là tam giác cân)
Vậy \(\Delta ABH=\Delta ACH\) (c.g.c)
b) Xét hai tam giác NBH và MCH ta có:
- NB = MC (vì AB = AC, M là trung điểm của AC và N là trung điểm của AB)
- HB = HC (đã chứng minh trên)
- \(\widehat{B}=\widehat{C}\) (đã chứng minh trên)
Suy ra \(\Delta NBH=\Delta MCH\) (c.g.c)
Khi đó HN = HM (vì hai cạnh tương ứng)
tam giác ABC cân tại A,H là trung điểm của BC
a.Chứng minh tam giác ABH =tam giác AHC và AH vuông góc với BC
b,kẻ HM vuông góc với AC tại M, kẻ HN vuông góc với AC tại N.Chứng minh tam giác AHM=Tam giác AHN
c. Gọi I là giao điểm của MH và AC,K là giao điểm của NH và AB. Chứng minh tam giác AIK là tam giác cân
`#3107.101107`
`a,`
Xét $\triangle ABH$ và $\triangle ACH$:
`AB = AC` $(\triangle ABC$cân tại A`)`
\(\widehat{B}=\widehat{C}\) $(\triangle ABC$cân tại A`)`
`HB = HC ( H` là trung điểm của BC`)`
$=> \triangle ABH = \triangle ACH (c - g - c)$
Vì $\triangle ABH = \triangle ACH$
`=>`\(\widehat{AHB}=\widehat{AHC}\left(\text{2 góc tương ứng}\right)\)
Mà `2` góc này nằm ở vị trí kề bù
`=>` \(\widehat{AHB}+\widehat{AHC}=180^0\)
`=>` \(\widehat{AHB}=\widehat{AHC}=\dfrac{180^0}{2}=90^0\) `=> AH \bot BC`
`b,`
Vì $\triangle ABH = \triangle ACH (a)$
`=>`\(\widehat{BAH}=\widehat{CAH}\left(\text{2 góc tương ứng}\right)\)
Xét $\triangle AHM$ và $\triangle AHN$:
AH chung
\(\widehat{MAH}=\widehat{NAH}\left(CMT\right)\)
\(\widehat{AMH}=\widehat{ANH}\left(=90^0\right)\)
$=> \triangle AHM = \triangle AHN (ch - gn)$
`c,`
Xét $\triangle HMB$ và $\triangle HNC$:
\(\widehat{HMB}=\widehat{HNC}\left(=90^0\right)\)
`HB = HC` `(`gt`)`
\(\widehat{HBM}=\widehat{HCN}\) $(\triangle ABC$ cân tại A`)`
$=> \triangle HMB = \triangle HNC (ch - gn)$
`=>`\(\widehat{BHM}=\widehat{CHN}\left(2\text{ góc tương ứng}\right)\) `(1)`
Vì \(\left\{{}\begin{matrix}\widehat{MHB}+\widehat{KHB}=\widehat{MHK}\\\widehat{NHC}+\widehat{IHC}=\widehat{NHI}\end{matrix}\right.\)
Mà \(\widehat{MHK}=\widehat{NHI}\left(\text{đối đỉnh}\right)\) `(2)`
Từ `(1)` và `(2)` `=>` \(\widehat{KHB}=\widehat{IHC}\)
Xét $\triangle KHB$ và $\triangle IHC$:
\(\widehat{KBH}=\widehat{ICH}\left(\widehat{ABC}=\widehat{ACB}\right)\)
`HB = HC`
\(\widehat{KHB}=\widehat{IHC}\)
$=> \triangle KHB = \triangle IHC (g - c - g)$
`=> BK = CI` `(2` cạnh tương ứng`)`
Ta có:
`AK = AB + BK`
`AI = AC + CI`
Mà `AB = AC; BK = CI`
$=> AK = AI => \triangle AIK$ cân tại A.
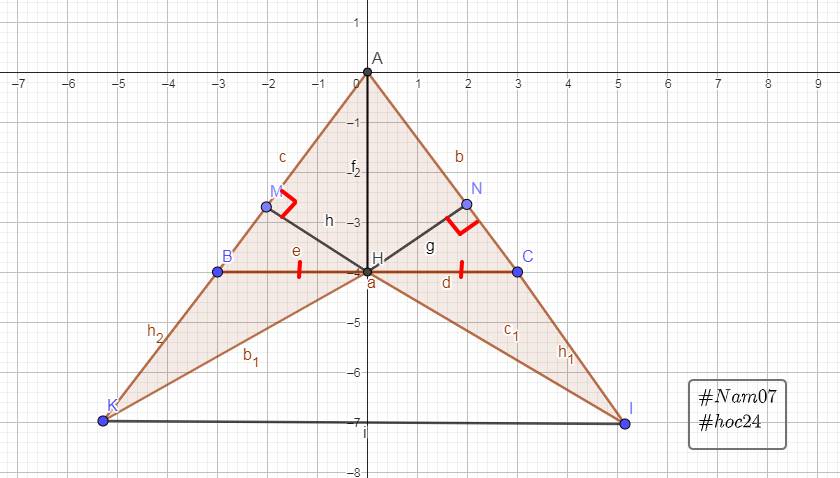
Cho tam giác ABC cân tại A. Đường cao AH (H thuộc BC).
a) Chứng minh H là trung điểm của BC và góc BAH = góc HAC.
b) Kẻ HM vuông góc với AB tại M và HN vuông góc với AC tại N. Chứng minh tam giác AMN cân tại A.
c) Vẽ P sao cho H là trung điểm đoạn NP. Chứng minh AH, MN, DP đồng quy.
d) MP cắt BC tại K, NK cắt MH tại D. Chứng minh AH, MN, DP đồng quy.
a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
=>ΔAHB=ΔAHC
=>HB=HC và góc BAH=góc CAH
b: Xét ΔAMH vuông tại M và ΔANH vuông tại N có
AH chung
góc MAH=góc NAH
=>ΔAMH=ΔANH
=>AM=AN
=>ΔAMN cân tại A
Cho tam giác ABC cân tại A. Điểm H là trung điểm của cạnh BC.
a) CM tam giác AHB = tam giác AHC. CM AH vuông góc với BC.
b) Kẻ HM vuông góc với AB tại M, kẻ HN vuông góc với AC tại N. CM tam giác AHM = tam giác AHN.
c) Gọi I là giao điểm của MH và AC, gọi K là giao điểm của NH và AB. CM tam giác AIK là tam giác cân.
a) Xét \(\Delta AHB\)và\(\Delta AHC\)có :
\(\hept{\begin{cases}HB=HC\\AH\\AB=AC\end{cases}}\)( Bạn tự ghi lời giải thích nha)
\(\Rightarrow\Delta AHB=\Delta AHC\left(c.c.c\right)\)
\(\Rightarrow\widehat{AHB}=\widehat{AHC}\)(2 cạnh tương ứng)
Mà \(\widehat{AHB}+\widehat{AHC}=180^o\)( 2 góc kề bù )
\(\Rightarrow\widehat{AHB}=\widehat{AHC}=\frac{180^o}{2}=90^o\)
\(\Rightarrow AH\perp BC\)
b) Xét \(\Delta AHM\left(\widehat{AMH}=90^o\right)\)và \(\Delta AHN\left(\widehat{ANH}=90^o\right)\)có :
\(\hept{\begin{cases}AH\\\widehat{A_1}=\widehat{A_2}\end{cases}}\)( bạn tự nêu lí do )
\(\Rightarrow\Delta AHM=\Delta AHN\)( Cạnh huyền - góc nhọn )
Bài tập:
Bài 1: Cho D ABC cân tại A. Vẽ AH vuông góc với BC tại H, có AB = 5cm, BC = 6cm.
1) Chứng minh hai tam giác ABH và ACH bằng nhau
2) Tìm độ dài đoạn AH?
c) Hãy cho biết trong tam giác trên AH là đường nào trong các đường sau: đường trung tuyến, đường cao, đường phân giác, đường trung trực?
Bài 2: Cho tam giác ABC cân tại A, gọi H là trung điểm của cạnh BC. Từ H vẽ HM vuông góc AB tại M, HN vuông AC tại N.
a) Chứng minh hai tam giác ABH và ACH bằng nhau
b) Chứng minh HM = HN
c) Chứng minh AM = AN
d) AH có là đường trung trực của tam giác ABC hay không? Vì sao?
Bài 3: Cho tam giác ABC có ba góc nhọn, vẽ hai đường cao AD và BE cắt nhau tại H. Cho biết góc ACB = 50 độ.
a) Chứng minh CH vuông góc AB
b) Tính góc BHD và góc DHE?
Bài 4: Cho tam giác ABC vuông tại A, BD là tia phân giác của góc B, trên tia BC lấy điểm E sao cho BA = BE, gọi H là giao điểm của AB với DE.
a) Chứng minh DE vuông góc BE
b) Chứng minh BD là đường trung trực của AE
c) Chứng minh AE song song với HC.
a) Xét ΔABN và ΔACM có
AB=AC(ΔABC cân tại A)
\(\widehat{BAN}\) chung
AN=AM(gt)
Do đó: ΔABN=ΔACM(c-g-c)
Suy ra: BN=CM(hai cạnh tương ứng)
b) Xét ΔAHB và ΔAHC có
AB=AC(ΔABC cân tại A)
AH chung
HB=HC(H là trung điểm của BC)
Do đó: ΔAHB=ΔAHC(c-c-c)
Suy ra: \(\widehat{AHB}=\widehat{AHC}\)(hai góc tương ứng)
mà \(\widehat{AHB}+\widehat{AHC}=180^0\)(hai góc kề bù)
nên \(\widehat{AHB}=\widehat{AHC}=\dfrac{180^0}{2}=90^0\)
hay AH⊥BC(đpcm)
c) Ta có: AH⊥BC(cmt)
mà H là trung điểm của BC(gt)
nên AH là đường trung trực của BC
⇔EH là đường trung trực của BC
⇔EB=EC(Tính chất đường trung trực của một đoạn thẳng)
Xét ΔEBC có EB=EC(cmt)
nên ΔEBC cân tại E(Định nghĩa tam giác cân)