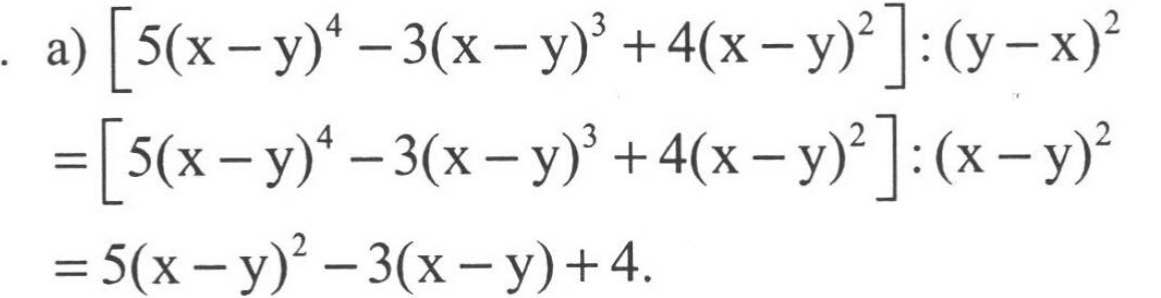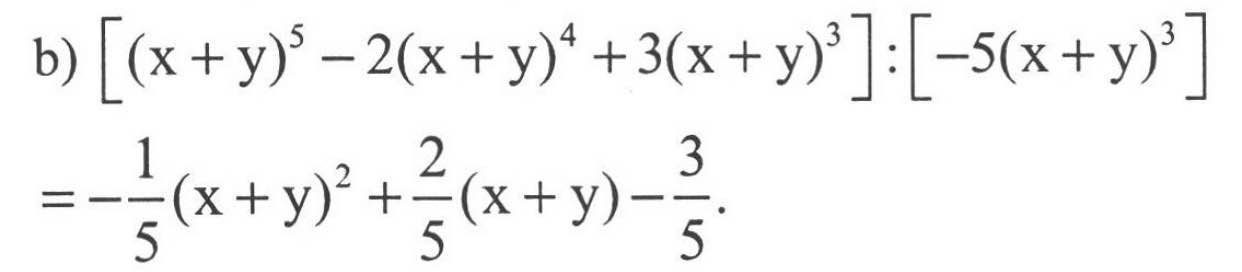Khai triển rồi thu gọn

đối với các câu này bạn hãy khai triển phần nào dài bằng hàng dẳng thức rồi thu gọn lại nếu đúng thì vế trái bằng vế phải

Đây nhé tích giúp mình nha

A nhé

Chọn A

Bạn cần phần nào thì mình sẽ giúp đỡ . Chứ bạn nhắn nhiều bài mình không giải được á . Chứ còn dạng bài như này thì hầu hết bạn đều phải nhân bung ra rồi rút gọn đi á .

muốn rối cái não bạn nhắn một lượt mình đọc không hiểu bạn nhắn từng câu thôi

vd câu 1:
ta có x-y=4 =>x=4+y
ta có pt:
4+y/y-2=3/2
=>8+2y=3y-6
=>-y=-14
=>y=14
=>x=4+y=4+14=18
các bài khác cũng tương tự thôi bạn

dấu chéo có nghĩa là phân số hí

Vậy đề bài yêu cầu gì vậy bạn?

`@` `\text {Ans}`

`\downarrow`

`1,`

\((y-5)(y+8)-(y+4)(y-1)\)

`= y(y+8) - 5(y+8) - [y(y-1) + 4(y-1)]`

`= y^2+8y - 5y - 40 - (y^2-y + 4y - 4)`

`= y^2+8y-5y-40 - y^2+y-4y+4`

`= (y^2-y^2)+(8y-5y+y-4y) +(-40+4)`

`= -36`

Vậy, bt trên không phụ thuộc vào gtr của biến.

`2,`

\(y^4-(y^2+1)(y^2-1)\)

`= y^4 - [y^2(y^2-1)+y^2-1]`

`= y^4- (y^4-y^2 + y^2-1)`

`= y^4-(y^4-1)`

`= y^4-y^4+1`

`= 1`

Vậy, bt trên không phụ thuộc vào gtr của biến.

`3,`

\(x(y-z) + y(z-x) +z(x-y)\)

`= xy-xz + yz - yx + zx-zy`

`= (xy-yx) + (-xz+zx) + (yz-zy)`

`= 0`

Vậy, bt trên không phụ thuộc vào gtr của biến.

`4,`

\(x(y+z-yz) -y(z+x-xz)+z(y-x)\)

`= xy+xz-xyz - yz - yx + yxz + zy - zx`

`= (xy-yx)+(xz-zx)+(-xyz+yxz)+(-yz+zy)`

`= 0`

Vậy, bt trên không phụ thuộc vào gtr của biến.

`5,`

\(x(2x+1)-x^2(x+2)+x^3-x+3\)

`= 2x^2+x - x^3 - 2x^2 + x^3 - x + 3`

`= (2x^2-2x^2)+(-x^3+x^3)+(x-x)+3`

`= 3`

Vậy, bt trên không phụ thuộc vào gtr của biến.

`6,`

\(x(3x-x+5)-(2x^3+3x-16)-x(x^2-x+2)\)

`= 3x^2 - x^2 + 5x - 2x^3 - 3x + 16 - x^3 + x^2 - 2x`

`= -3x^3 + 3x^2 + 16`

Bạn xem lại đề bài.

`\text {#KaizuulvG}`

3) \(\Rightarrow\dfrac{x}{5}=\dfrac{y}{9}=\dfrac{x-y}{5-9}=\dfrac{-40}{-4}=10\)

\(\Rightarrow\left\{{}\begin{matrix}x=10.5=50\\y=10.9=90\end{matrix}\right.\)

4) \(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{5x}{10}=\dfrac{2y}{6}=\dfrac{5x-2y}{10-6}=\dfrac{28}{4}=7\)

\(\Rightarrow\left\{{}\begin{matrix}x=7.2=14\\y=7.3=21\end{matrix}\right.\)

5) \(\dfrac{x}{5}=\dfrac{y}{7}=\dfrac{z}{10}=\dfrac{x+y-z}{5+7-10}=\dfrac{20}{2}=10\)

\(\Rightarrow\left\{{}\begin{matrix}x=10.5=50\\y=10.7=70\\z=10.10=100\end{matrix}\right.\)

6) \(\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{z}{5}=\dfrac{3x}{9}=\dfrac{2y}{8}=\dfrac{2z}{10}=\dfrac{3x-2y+2z}{9-8+10}=\dfrac{121}{11}=11\)

\(\Rightarrow\left\{{}\begin{matrix}x=11.3=33\\y=11.4=44\\z=11.5=55\end{matrix}\right.\)

7) \(\Rightarrow\dfrac{x}{12}=\dfrac{y}{6}=\dfrac{z}{10}=\dfrac{x+y-z}{12+6-10}=\dfrac{20}{8}=\dfrac{5}{2}\)

\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{5}{2}.12=30\\y=\dfrac{5}{2}.6=15\\z=\dfrac{5}{2}.10=25\end{matrix}\right.\)

Câu 3:

\(\dfrac{x}{y}=\dfrac{5}{9}\Rightarrow\dfrac{x}{5}=\dfrac{y}{9}\)

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

\(\dfrac{x}{5}=\dfrac{y}{9}=\dfrac{x-y}{5-9}=\dfrac{-40}{-4}=10\)

\(\dfrac{x}{5}=10\Rightarrow x=5\\ \dfrac{y}{9}=10\Rightarrow y=90\)

Câu b:

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{5x-2y}{10-6}=\dfrac{28}{4}=7\)

\(\dfrac{x}{2}=7\Rightarrow x=14\\ \dfrac{y}{3}=7\Rightarrow y=21\)

Câu c:

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

\(\dfrac{x}{5}=\dfrac{y}{7}=\dfrac{z}{10}=\dfrac{x+y-1}{5+7-10}=\dfrac{20}{2}=10\)

\(\dfrac{x}{5}=10\Rightarrow x=50\\ \dfrac{y}{7}=10\Rightarrow y=70\\ \dfrac{z}{10}=10\Rightarrow z=100\)

Câu d:

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

\(\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{z}{5}=\dfrac{3x-2y+2z}{9-8+10}=\dfrac{121}{11}=11\)

\(\dfrac{x}{3}=11\Rightarrow x=3\\ \dfrac{y}{4}=11\Rightarrow y=44\\ \dfrac{z}{5}=11\Rightarrow z=55\)

Câu e:

\(\dfrac{x}{4}=\dfrac{y}{2}\Rightarrow\dfrac{x}{8}=\dfrac{y}{6}\\\dfrac{y}{3}=\dfrac{z}{5}\Rightarrow\dfrac{y}{6}=\dfrac{z}{10}\\ \Rightarrow\dfrac{x}{8}=\dfrac{y}{6}=\dfrac{z}{10} \)

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

\(\dfrac{x}{8}=\dfrac{y}{6}=\dfrac{z}{10}=\dfrac{x+y-z}{8+6-10}=\dfrac{20}{4}=5\)

\(\dfrac{x}{8}=5\Rightarrow x=40\\ \dfrac{y}{6}=5\Rightarrow y=30\\ \dfrac{z}{10}=5\Rightarrow z=50\)

`Answer:`

\( B=-4x^5.y+x^4.y^3-3x^2.y^3.z^2+4.x^5.y-2.y^4-x^4.y-x^4.y+3.y^4+4.y^2.x^2.z^2-y^4+\frac{1}{2}\)

\(=-4x^5y-3x^2y^3z^2+4x^y-2y^4+3y^4+4x^2y^3z^2-y^4+\frac{1}{2}\)

\(=-4x^5y+x^2y^3z^2+4x^y-2y^4+3y^4-y^4+\frac{1}{2}\)

\(=-4x^5y+x^2y^3z^2+4x^y+\frac{1}{2}\)

B=-4x^5y+x^4y^3-3x^2y^3z^2+4x^5y-2y^4-x^4y-x^4y+3y^4+4y^2x^2z^2-y^4+\(\frac{1}{2}\)

  =(-4x^5y+4x^5y)+x^4y^3-3x^2y^3z^2+(2y^4+3y^4-y^4)+(-x^4y-x^4y)+4y^2x^2z^2+\(\frac{1}{2}\)

  =x^4y^3-3y^3z^2-2x^4y+4y^2x^2z^2+\(\frac{1}{2}\)

ban oi mau tra loi di